معرفی الگوریتم BatchNormalization
بسم الله الرحمن الرحیم
در این پست قصد داریم بصورت مروری با الگوریتم بچ نرمالیزیشن آشنا بشیم. بچ نرمالیزیشن یا همون اصطلاحا بچ نرم یکی از تاثیرگذارترین الگوریتم ها (تو حوزه نرمالسازی ) بود که تاثیر بسیار زیادی بر روی ترینینگ استیبل و راحت تر معماری های عمیق گذاشت.
ایده بچ نرمالیزیشن رو میشه از دو جهت بررسی کرد .یک ایده بر میگیرده به شهودی که در معماری ها و کارهای سابق حاصل شد. یعنی قبلا به یک نکته مشترک بین همه معماری های قبلی رسیده بودیم و اون هم بحث نرمال سازی داده ورودی به شبکه بود. و دیدم که تمام معماری ها گزارش دادند که که اینکار باعث تسریع همگرایی میشه.
اینکه چرا این کار باعث تسریع همگرایی میشه دلایل مختلفی داره که در گارگاه بهش اشاره شد. دیدیم که وقتی نرمالسازی انجام میشه اسکیل های مختلف متناسب میشن و در نتیجه اگر نگاهی به کانتور مقادیر پارامترها و خطای شبکه بندازیم و اون رو قبل و بعد از نرمالسازی با هم مقایسه کنیم مشاهده میکنیم که این کانتور بیشتر به یک دایره شبیه شده(نسبت به یک بیضی) و در این حالت الگوریتم گردایان دیسنت خیلی سریعتر میتونه پیش بره و اصطلاحا فلاکچویشن کمتری خواهد داشت.(حرکت زیگزاکی کمتری خواهد داشت.) . علاوه بر این قضیه در توابع اشباع شونده هم این موضوع باعث میشه تا دیرتر این نوع توابع در نواحی اشباع شدگی قرار بگیرن و در نتیجه فرایند آموزش دیرتر دست به گریبان مشکلاتی مثل vanishing gradient بشن و گرادیان ها مقادیر متناسب تری برای مدت زمان بیشتری داشته باشن. و گفتیم ایده دیگه هم مربوط میشه به حذف اطلاعات کلی در ورودی تا اطلاعات پیچیده تر (ساختارهایپیچیده تر) در ورودی مشخص تر قابل ارائه به شبکه بشن و اینطور بهتر بشه ویژگی های منحصر به فرد هر کلاس رو بدست اورد و تمییز داد.
با توجه به صحبتهایی که تا بحال شد، سوالی مطرح میشه مبنی بر اینکه چی میشد اگه ورودی هر لایه رو هم نرمال میکردیم؟ ایا بنظر شما این کار باعث تسریع بیشتر همگرایی نمیشه؟
این یک یک روی سکه از بحثی هست که باهاش مواجه ایم . روی دیگر سکه برمیگیرده به بحثی که ازش بنام Covariate shift نام برده شده. حالا این چی هست؟
Covariate shift به تغییر توزیع ورودی در یک سیستم یادگیری اشاره داره . زمانی که توزیع ورودی به یک سیستم تغییر کنه ما اصطلاحا میگیم اون سیستم در حال تجربه Covariate shift هست.
این بحث تغییر توزیع ورودی رو میشه علاوه بر کل سیستم به زیربخشهای اون هم تعمیم داد. یعنی ما میتونیم در یک زیرشبکه و یا در یک لایه و باز حتی در سطح یک نورون هم covariate shift یا همون تغییر توزیع رو داشته باشیم .
وقتی این اتفاق در سطح نورونها رخ بده اصطلاحا بهش میگیم internal covariate shift رخ داده.
اگه بخواییم این بحث covariate shift رو بازتر و عینی ترش کنیم نیازه چند مثال بزنیم .
ما میدونیم که توزیع داده یا همون Data distribution حاوی اطلاعات بسیار مهمی از نرخ رخدادها ،مقادیر مورد انتظار، رنج اونها و …. از داده ورودی ماست. با توجه به این توزیع داده است که ما تصمیم گیری میکنیم. بزارید عینی تر بشیم. شما برای اینکه بتونید برآورد مناسبی از واقعه ای داشته باشید نیازمند اون هستید که اطلاعات دقیقی در مورد اون کسب کنید. بعنوان مثال اگر در جایی زندگی میکنید که از جمعیت ۱۰۰ نفری ، ۷۰ نفر بشدت گرسنه و قحطی زده و در معرض مرگ و ۲۰ نفر بدون مسکن و ۱۰ نفر بدون مشکل باشن و قرار باشه شما تصمیمی در جهت رفع مشکلات بگیرید مشخصه که دقیق بودن این آمار چقدر در نتیجه تاثیر داره. تغییر امار باعث میشه نهایتا تصمیم متفاوتی گرفته بشه که شاید مورد انتظار نباشه. اگر امار دستکاری بشه یا بشکلی تغییر بکنه بطوری که تعداد صحیح قحطی زده ها با گرو های دیگه عوض بشه یک فاجعه رخ میده. هرچقدر این تغییرات از کم به سمت بیشتر باشه مشخصه که تصمیم گرفته شده در انتها با تصمیم مورد انتظار(صحیح) چقدر میتونه فاصله پیدا کنه.
در بحث تغییر توزیع هم ما با یک همچین مساله ای مواجه هستیم. میشه چیزی که در یک شبکه عصبی عمیق رخ میده رو به یک صف طولانی هم مثال زد .
در ابتدای صف یک فرد درخواستش رو به نفرد بعدی میگه و اون هم به بعدی و اون هم به بعدی و… تا اینکه به انتهای صف برسه و درخواست نفر اول ارائه بشه و نهایتا از انتهای صف درخواستش اجابت بشه.
فرض کنید یک فرد در ابتدای صف میگه : من نون میخوام. فرد بعدی به نفر بعدش میگه “قبلی نون میخواد” ، بعدی هم میگه ” قبلی نون میخواد” بعدی “قبلی نون میخواد” ، نفر بعد اما میشنوه “قلی نون میخواد” به بعدی میگه “قلی نون میخواد” و… این پروسه تکرار میشه
تا اینکه نهایتا از “قبلی نون میخواد” به قلی نون میخواد” ، قلی دون میخواد” ، قلی دم میخواد! و… میرسه و نهایتا پیام ابتدایی با چیزی که در انتها به مقصد میرسه کاملا متفاوت هست.
از نون رسیدیم به دون! و به دم! (اینجا مثلا بخاطر بد شنیدن اطلاعات تغییر پیدا کرده)
(چیزی که اینجا مشهوده اینه که اگه تعداد کم باشه میزان این تغییرات هم خیلی کم میتونه باشه نسبت به زمانی که صف ، خیلی طولانی تر باشه یک اشتباه رفته رفته بیشتر و بزرگتر میشه تاثیرش )

میشه قضیه یک کلاغ چهل کلاغ رو هم مثال زد که هرچقدر پیش بره اتفاقی که رخ داده در ابتدا با چیزی که در انتها پیش میره خیلی متفاوت هست . امیدوارم ایده گرفته باشید و متوجه منظور من شده باشید (اگر نه در کامنت بگید تا بازتر بشه)
همینطور مثال فنی تری اگر بخواییم بزنیم میشه به این اشاره کرد که شما بعنوان مثال در زمان ترین مدلتون از یک سری تصاویر استفاده کنید (مثلا سیاه و سفید و یک نوع گربه خاص و یا فقط تحت یک شکل یا زاویه خاص و…) اما در زمان تست از تصاویر رنگی و انواع گوناگون گربه ها (یا کلا با تغیراتی که در داده اموزشی نبوده) برای تست مدل استفاده کنید. اینجا چون توزیع داده تست و اموزش شما متفاوت هست مدل شما کارایی خیلی بدی ارائه خواهد داد.
بعنوان مثال شما در آموزش از تصاویری به این صورت استفاده کنید:
اما در زمان تست تصاویری بصورت زیر داشته باشید
در نهایت به این میرسیم که بحث توزیع بحث بسیار با اهمتیه و در اصل چیزی که باعث میشه سیستم های فعلی ما که مبتنی بر Empirical risk minimization هستن بدرستی کار کنن حداقل بودن تفاوت در توزیع داده (در زمان اموزش با زمان تست) هست و اگر این اصل رعایت نشه کلا قابلیت استفاده اونها زیرسوال میره. (در پستی جداگانه انشاءالله در این باره بیشتر ضحبت میکنم)
برگردیم سر شبکه های عصبی . این قضیه چطوری به شبکه های عصبی ارتباط پیدا میکنه ؟
شبکه های عصبی ما متشکل از چند لایه پشت سر هم هستند. تنها لایه اول با داده ما (توزیع اصلی) برخورد مستقیم داره و مابقی لایه ها بصورت غیرمستقیم به این اطلاعات دسترسی دارن . همه اینها یعنی چی؟
یعنی فعل و انفعالاتی که در لایه های اول صورت میگیره باعث اعمال تغییرات در توزیع داده ورودی به شبکه میشه و وقتی عمق زیاد باشه، این تاثیرات انقدر زیاد میشن که باعث میشن در لایه های بالاتر توزیع ورودی دستخوش تغییرات زیادی بشه. بعبارت دیگه وزنها و پارامترهای قبلی همه روی ورودی ای که به یک لایه در عمق X میرسه تاثیر میگذارن و اینها مشکل ایجاد میکنن.
این مساله به نوبه خودش مشکلات جانبی دیگه ای رو هم باعث میشه . از اون جمله میشه به حساسیت بالا به مقداردهی اولیه شبکه، سخت و طاقت فرسا شدن کار با توابع غیرخطی اشباع شونده (مثل بحث اشباع شدگی سریع این نوع توابع غیرخطی) و نهایتا کاهش سرعت همگرایی بعلت انتخاب نرخ یادگیری بسیار کمتر تا بخاطر مسائل قبلی واگرایی شبکه رخ نده.
بچ نرمالیزیشن برای حل این مشکل(بطور خاص کاهش این تغییر توزیع) ارائه شده. با استفاده از بچ نرمالیزیشن شبکه حساسیت کمتری به مقداردهی اولیه وزنها خواهد داشت و همینطور از نرخ یادگیری به مراتب بالاتری میشه استفاده کرد. همینطور با استفاده از بچ نرمالیزیشن از توابع اشباع شونده مثل سیگموید و tanh هم میشه استفاده کرد و با مشکلاتی نظیرvanishing gradient و…مواجه نشد. همچنین بچ نرمالیزیشن نقش یک رگیولایزر رو هم ایفا میکنه که در ادامه بیشتر توضیح میدم
بزارید اینو عینی ترش کنیم
اگه فرض کنیم داده ورودی ما در یک شبکه عصبی (کم عمق) بفرم زیر باشه با نرمالسازی(در ورودی) ما به چیزی که میخواییم دست پیدا میکنیم و نیاز به انجام نکته خاص دیگه ای نداریم.
منتها اگر لایه های زیادی داشته باشیم به مثابه این میمونه توزیع داده ورودی دائما تغییر میکنه.حالا چطوری؟ اجازه بدید کمی عینی ترش کنیم:
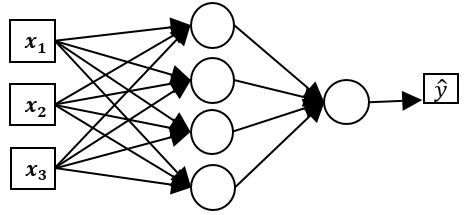
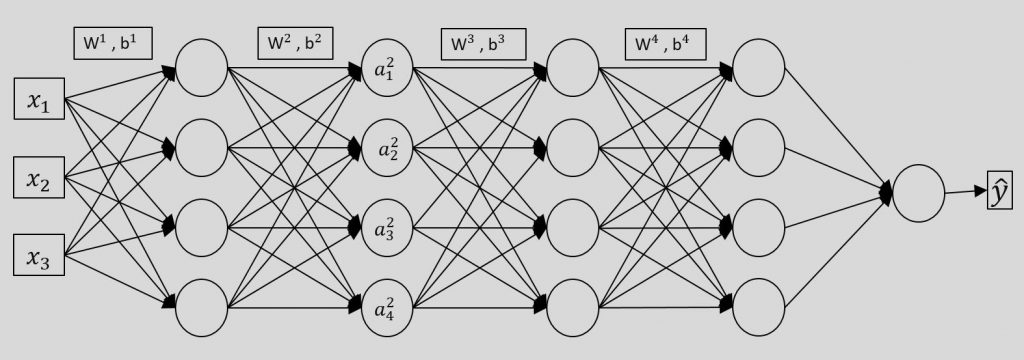 در تصویر بالا فرض کنید ما بخواییم پارامترهای W3 , b3 رو تنظیم کنیم . لایه سوم ما یکسری ورودی داره که ما بهش میگیم a1 الی a4 . اگه بخواییم از دید لایه سوم به شبکه نگاه کنیم بصورت زیر خواهد بود :
در تصویر بالا فرض کنید ما بخواییم پارامترهای W3 , b3 رو تنظیم کنیم . لایه سوم ما یکسری ورودی داره که ما بهش میگیم a1 الی a4 . اگه بخواییم از دید لایه سوم به شبکه نگاه کنیم بصورت زیر خواهد بود :
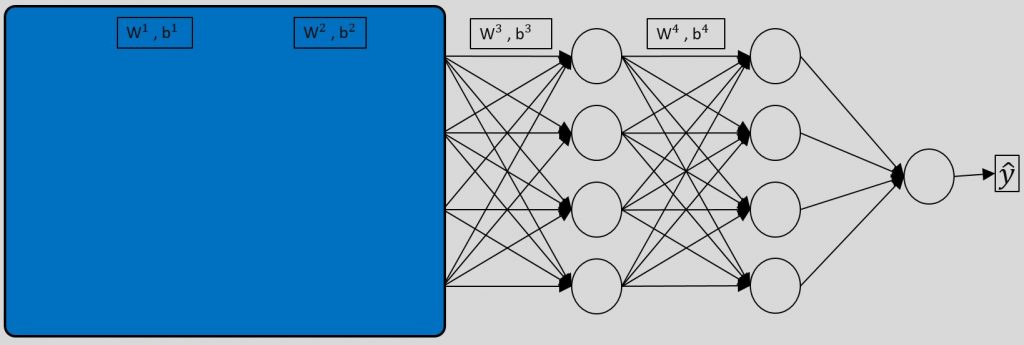 یعنی لایه سوم کاری به لایه های قبلی و… نداره . اون میگه من صرفا یکسری ورودی دارم و بر اساس مقادیر اونها (توزیع داده اونها) پارامترهام (W3,b3) رو تنظیم میکنم . تا اینجا هیچ مشکلی نیست. مشکل از جایی شروع میشه که مقادیر a1 تا a4 (قبل از ورود به تابع فعالسازی) وابسته به مقادیر و پارامترهای قبلی هستن. یعنی اونها خروجی لایه قبلی هستن که با داده ورودی و ضرب و جمع وزنها و بایاس ها از لایه های قبلی مقادیرشون کاملا دستخوش تغییر میشه.( نه تنها داده ورودی داره ، بلکه پارامترهای قبلی هم بعنوان ورودی لحاظ میشن) به همین صورت شبکه مجبوره بطور مکرر خودش رو با تغییرات در توزیع ورودیش در تطبیق بده. اینجاست که با تفاوت اسکیل در مقادیر ورودی و همینطور لایه های بیشتر، تغییرات در لایه های ابتدایی تاثیرات خیلی بیشتری در لایه های انتهایی میزارن. برای همین برای رفع این مشکل و کاهش میزان تغییرات ما میاییم ورودی ها رو نرمال میکنیم .
یعنی لایه سوم کاری به لایه های قبلی و… نداره . اون میگه من صرفا یکسری ورودی دارم و بر اساس مقادیر اونها (توزیع داده اونها) پارامترهام (W3,b3) رو تنظیم میکنم . تا اینجا هیچ مشکلی نیست. مشکل از جایی شروع میشه که مقادیر a1 تا a4 (قبل از ورود به تابع فعالسازی) وابسته به مقادیر و پارامترهای قبلی هستن. یعنی اونها خروجی لایه قبلی هستن که با داده ورودی و ضرب و جمع وزنها و بایاس ها از لایه های قبلی مقادیرشون کاملا دستخوش تغییر میشه.( نه تنها داده ورودی داره ، بلکه پارامترهای قبلی هم بعنوان ورودی لحاظ میشن) به همین صورت شبکه مجبوره بطور مکرر خودش رو با تغییرات در توزیع ورودیش در تطبیق بده. اینجاست که با تفاوت اسکیل در مقادیر ورودی و همینطور لایه های بیشتر، تغییرات در لایه های ابتدایی تاثیرات خیلی بیشتری در لایه های انتهایی میزارن. برای همین برای رفع این مشکل و کاهش میزان تغییرات ما میاییم ورودی ها رو نرمال میکنیم .
کاری که ما با بچ نرمالیزیشن میکنیم کاهش میزان این تغییرات هست. ما داریم میگیم که هرچند داده دارای تغییراتی بوده اما میانگین و واریانس اون مقدار ثابتی هست و تغییرات انچنانی نداره . پس با این کار ما اومدیم تاثیرات پارامترهای قبلی و همینطور شرایط تاثیرگذار روی اونها رو کاهش دادیم . در حالت عادی اگر مقداردهی اولیه برفرض مثال مقدار زیادی بود این میتونست در مقادیر بعدی تغییرات زیادی رو بوجود بیاره اما در حال حاضر ما حساسیت خیلی کمتری نسبت به این مساله داریم .با نرمالسازی ورودی در سطح هر لایه، هنوز تغییرات داریم اما این تغییرات خیلی کمتر از حالت معمول هست. تصاویر زیر بنوعی سعی دارن این مساله رو نشون بدن. دو تصویر اول حالت معمول بدون نرمالسازی رو شبیه سازی میکنن و تصویر اخر (سمت راست) هم بعنوان مثال وضعیت نرمال شده رو نشون میده
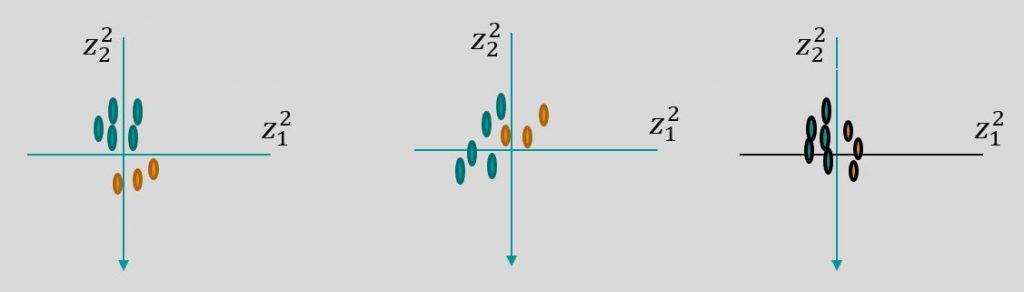
همینطور اگر برفرض مثال از توابع اشباع شونده مثل سیگموید استفاده میکردیم خیلی سریع اونها بخاطر مقادیر بزرگ به حدود اشباع خودشون نزدیک میشدن و اموزش خیلی کند میشد چون گردایان کوچک میشد (چون مقادیر در بخشهای حدی کوچک شده بودن) . با اینکار در این نوع توابع هم ما از بخشهای حدی فاصله میگیریم و از بخش میانی که گرادیان مناسبی بدست میده میتونیم بیشتر استفاده کنیم (دلیلش هم اینه که اعداد بزرگ و اعداد خیلی کوچک تاثیراتشون بخاطر نرمالسازی متعادل میشه (دقت کنید بحث ما در لایه های عمیق شبکه اس ))
خب این همه صغری کبری چیدیم که به این برسیم که نرمالسازی در سطح هر لایه انجام بشه و این خوبه. اما فرمولی که در بچ نرمالیزیشن وارد شده یکسری پارامتر عجیب مثل گاما و بتا داره! دلیل وجود اینها چیه ؟
اگه ما بیاییم و سعی کنیم خیلی معمولی مقادیر همه لایه ها رو نرمال کنیم میبینیم شبکه واگرا میشه! و این به این معناست که در بعضی جاها نباید عمل نرمالسازی انجام بشه . ممکنه بپرسید چطور همچین چیزی ممکنه ؟ چطور یکجا ما میگیم باید توزیع ورودی حفظ بشه اما بعدش میگیم نه نباید حفظ بشه ؟ هرچی حساب شده همون استفاده بشه ؟
داده ورودی در طی مسیرش دستخوش تبدیلات مختلفی میشه و چیزی که در وسط یا انتهای شبکه وجود داره اون چیزی نیست که در ابتدا به شبکه ارائه شده. بعبارت بهتر ما از یک رپرزنتیشن به رپرزنتیشن دیگه ای میرسیم. از یک سطح انتزاع به سطح انتزاع دیگه ای میرسیم. در اینجا از یک لایه به بعد لایه میگه من یک ورودی دریافت کردم و یک خروجی تولید کردم تو از این چیزی که من تولید کردم استفاده کن کاری به قبل نداشته باش. این اون داده اصلی هست که از این به بعد باهاش سرو کار دارید تصمیم گیری هاتون مبتنی بر این باید باشه. بنابر این وقتی به این موارد میرسیم شبکه باید بتونه بدون اینکه عمل نرمالسازی رو انجام بده داده رو به لایه بعد ارائه کنه. یا اگر داده ای رو نرمال کرد و دید نتیجه بدتر شد باید بتونه بطوری عکسش رو انجام بده و نرمالسازی رو خنثی کنه. برای اینکار بطور خلاصه شبکه باید بتونه یک تابع همانی رو بدست بده. یعنی هر وقت قرار بر نرمالسازی نبود فرمول مربوط به بچ نرمالیزیشن کار تابع همانی رو انجام بده (یعنی بدون تغییر در ورودی عینا اون رو در خروجی ارائه کنه) . کار گاما و بتا همین هست.
اگر گاما برابر با مقدار sqrt(var(x)) و بتا برابر با مقدار mean(x) باشه عمل نرمالسازی خنثی میشه و به این ترتیب جاهایی که نیاز به نرمالسازی هست نرمال شده و جاهایی هم که نیاز نیست این کار صورت نمیگیره .
یک نکته از اونجایی که نرمالسازی نسبت به تمامی دیتاست غیرممکن هست ما عمل نرمالسازی رو نسبت به هر بچ انجام میدیم که همین مساله باعث ارائه یکسری ویژگی های جالب توجه میشه که درادامه بهش میپردازیم .
مرور:
خب حالا بزارید یک خلاصه ای داشته باشیم از بحثایی که کردیم :
گفتیم مشکل اینجاست که فرایند اموزش بخاطر این مساله که ورودی هر لایه توسط پارامترهای تمامی لایه های قبلی تحت تاثیر قرار میگیره بغرنج و پیچیده میشه. چرا که تغییرات کوچک در پارامترهای شبکه با عمیقتر شدن شبکه تاثیرشون چندین برابر میشه.
این تغییرات در توزیع ورودی لایه ها یه مشکلی رو ایجاد میکنه چون لایه ها بطور دائم باید خودشون رو با توزیع جدید تطبیق بدن. زمانی که توزیع ورودی به یک سیستم یادگیری تغییر کنه ما اصطلاحا میگیم covariate shift اتفاق افتاده .
البته این مساله covariate shift رو میشه فرای کل سیستم ، برای بخشهای مختلف اون مثل زیر شبکه یا یک لایه هم در نظر گرفت .
در نتیجه خصائص و ویژگی های توزیع ورودی که موجب بهینه سازی فرآیند آموزش میشه – مثل داشتن توزیع یکسان بین داده اموزش و تست- همین تاثیر رو بر روی زیرشبکه هم خواهد داشت. به همین صورت ثابت موندن توزیع x در طی زمان مفید فایده خواهد بود. چرا که با این شرط دیگه پارامترهایی مثل W که در لایه های عمیقتر شبکه هستن لازم نیستد که خودشون رو دائما با تغییرات ورودی وفق بدن .
ثابت بودن توزیع در یک زیرشبکه نتایج مثبتی برای لایه هایی که خارج از این زیرشبکه هستن داره . بعنوان مثال یک لایه ای رو در نظر بگیرید که از تابع سیگموید داره استفاه میکنه بصورت z = g(Wu+b) . که در اینجا u هم همون ورودی لایه ماست . W هم ماتریس وزن و b هم بایاست هست که جزو پارامترهای لایه است که باید یادگرفته بشن. و g(x) هم همون تابع سیگموید که بصورت زیر هست g(x) = 1/1+exp(-x) . با افزایش |x| مقدار g’(x) هم به سمت صفر میل میکنه . یعنی چی ؟ یعنی تقریبا برای تمامی ابعاد x= Wu+b جریان گرادیانی که به سمت u (ابتدای شبکه ) در حال حرکت هست رفته رفته کاهش پیدا میکنه و به همین دلیل اموزش بشدت کاهش سرعت پیدا میکنه. هرچند از اونجایی که x توسط w و b و تمامی پارامترها از لایه های قبلی تاثیر میپذیره ، تغییر در هر یکی از اون پارامترها در زمان اموزش احتمالا باعث حرکت تعداد زیادی از ابعاد x به سمت ناحیه اشباع شدگی تابع غیرخطی ما میشه و نهایتا همگرایی رو کاهش میده. این اثر بطور معمول با استفاده از مقداردهی ژاویر و استفاده از تابع غیرخطی رلو و انتخاب یک نرخ یادگیری کم معمولا سعی میشه برطرف بشه . حالا اگر ما بتونیم بنوعی اطمینان حاصل کنیم که توزیع ورودی به توابع غیرخطی ما بیشتر پایدار بمونن در حین اموزش شبکه، پس بهینه ساز میتونه کمتر در اون نواحی اشباع شدگی گیر بیوفته و در نتیجه اموزش تسریع میشه .
ما به این تغییر توزیع در نورونهای داخلی در درون یک شبکه عمیق میگیم اینترنال کورویت شیفت . حذف این مشکل یا کاهش اون باعث سرعت در اموزش میشه .
بچ نرم با ترمیم میانگین و واریانس ورودی لایه ها به این مهم دست پیدا میکنه . بچ نرمالیزیشن دارای یک اثر مفید بر روی جریان گرادیان در داخل شبکه است که این کار رو از طریق کاهش وابستگی گردایان ها به اسکیل پارامترها و یا مقادیر اولیه اونها انجام میده . این نکته باعث میشه بشه از نرخ یادگیری بیشتری استفاده کرد بدون نگرانی از ریسک واگرایی .
بنابر این با توجه به صحبتی که بالا کردیم با بچ نرم میشه از توابع سچریتینگ مثل سیگموید هم استفاده کرد .
(قبلا یان لیکون و دیگران هم اشاره کرده بودن که نرمالسازی داده ورودی و میانگین صفر و واریانس ۱ باعث تسریع اموز ش میشه .
حالا ایده اولیه هم این بوده که ورودی هر لایه رو به همین شکل نرمال کنیم تا نهایتا بسمت ثابت سازی توزیع ورودی هر لایه گام برداریم . این یک اشکالی داره و اون هم اینه که عملیات سربار زیادی داره و عملی نیست . برای همین ما بجای اینکه ویژگی ها در ورودی و خروجی یک لایه رو بصورت مشترک نرمال کنیم میاییم و هر ویژگی رو بصورت مستقل نرمال میکنیم (اونم با قرار دادن میانگین برابر صفر و واریانس ۱) که میشه بصورت زیر:
|
1 2 3 |
y(k) = γ(k)x^(k) + β(k) |
قبلا گفتیم که اینطوری ورودی هر لایه رو نرمال کنیم ممکنه اون چیزی که یک لایه داره سعی میکنه represent کنه رو تغییر بدیم . بعنوان مثال نرمالسازی ورودی یک سیموید ممکنه اونها رو محدود به یک ناحیه خطی از این تابع کنه. به منظور برطرف کردن این مشکل اینها هم تغییری در بچ نرم دادن تا بتونه تبدیل identity یا همانی رو هم انجام بده .
اینجاست که پارامترهای گاما و بتا معرفی میشن و مثل بقیه پارامترها یادگرفته میشن . اگر مقدار گاما برابر با sqrt(var(x)) و بتا هم برابر میانگین باشه ما اکتیویشن های اصلی رو بدست میاریم یا بعبارت دیگه تغییری در توزیع نمیدیم انگار که نرمالسازی انجام نشده .
اثر رگیولاریزیشن
در زمان آموزش با بچ نرمالیزیشن یک مثال به همراه سایر مثالها در داخل یک مینی بچ بهش نگاه میشه و دیگه اموزش شبکه یک جواب مشخص برای یک مثال اموزشی ایجاد نمیکنه . در نتیجه این حالت باعث تعمیم بهتر شبکه میشه . برای همین هم گفته میشه که میشه یا از دراپ اوت استفاده نکرد یا اگر میکنن تاثیرش رو کم کنن.
اثر بچ نرم در اجازه به استفاده از نرخ یادگیری بالاتر
نرخ یادگیری خیلی بالا باعث ایجاد اکسپلودینگ گریدینت یا ونیشینگ گریدینت میشه و همچنین باعث گیر افتادن در لوکال مینیمای بد. با استفاده از نرمالسازی اکتیویشن ها در سراسر شبکه باعث میشیم که تغییرات کوچیک در پارامترها باعث ایجاد تغییرات بزرگ و غیر بهینه در اکتیویشن ها و در گردایان ها نشه . بعنوان مثال از اموزش در گیر افتادن در نواحی اشباع شده توابع غیرخطی جلوگیری میشه . همچنین با بچ نرمالیزیشن اموزش نسبت به مقیاس یا اسکیل پارامترها هم قدرتمندتر و روباست تر میشه . بطور عادی نرخ یادگیری بالا ممکنه اسکیل پارامترهای یک لایه رو افزایش بده که این به نوبه خودش مقدار گرادیان رو در حین بک پراپگیشن افزایش میده و سبب انفجار مدل میشه . اما با بچ نرمالیزیشن بک پراپکیشن از داخل یک لایه دیگه نسبت به اسکیل پارامترها بی تاثیر میشه .
برای اثر بخشی بیشتر بچ نرمالیزیشن در نتیجه باید داده ها بیشتر شافل بشن . بعضی از الگوریتم ها بصورت رندوم هر بار دیتا رو شافل میکنن اینطور ممکنه یک سمپل در چند بچ باشه . برای اثر بخشی بیشتر این مساله باید در نظر گرفته بشه .
یادتون باشه بچ نرمالیزیشن سربار پردازشی اعمال میکنه چیزی در حدود ۳۰ درصد بقولی. قدیم مرسوم بود برای لایه های انتهایی صرفا بچ نرم رو لحاظ میکردن اما الان در همه لایه ها . اینو برای کاربرد خاصتون مورد نظر قرار بدید .
نکته دیگه اینکه بچ نرمالیزیشن یک خصوصیت رگیولاریزیشنی داره و زمانی که در شبکه خودتون استفاده اش کردید باید از مقادیر دراپ اوت کم کنید . خیلی ها بر اساس چیزی که در مقاله اقای هینتون اومده از نرخ ۵۰ درصد استفاده میکنن که این اشتباهه و در خیلی از موارد باعث اندرفیت شبکه میشه و باز برای جلوگیری از اون و بهتر شدن دقت تعداد پارامترها رو افزایش میدن و به این شکل سربار زیادی رو ایجاد میکنن. این مد نظر شما باشه .
و فکر میکنم مهمترین مواردی که بحث شد همین موارد بود. سعی کنید حتما مقاله اصلی رو مطالعه کنید با اطلاعاتی که اینجا هست باید بتونید براحتی مقاله رو بخونید و اگر با مطالب بالا سردرگم شدید سوال کنید(یا به مقاله اصلی مراجعه کنید احتمالا قضیه روشن میشه براتون)
من در ادامه سعی میکنم ویرایش مطالب رو بهتر کنم و توضیحات رو جاهایی که دوباره به ذهنم میاد بیشتر بسط بدم و یابخشهایی رو اگر گنگ بیان کردم بهتر بیان کنم.
تصاویر برگردفته از مقاله اصلی و اسلاید ارائه شده در کارگاه هست.










حسین آقا درود و سپاس از بابت مقاله خوب ومفیدتان
خیلی بهتر بود اصطلاحات انگلیسی را مثل رپرزنتیشن و .. مستقیم خود کلمه انگلیسیاش را مینوشتید اگر قابل ترجمه نبود.
باز هم از شما و زحمتی که برای این مقاله کشیدید و با ما به اشتراک گذاشتید سپاسگزارم.
سلام.
خواهش میکنم. قابل ترجمه که هستند من به معادلهای فارسی چندان مسلط نیستم و با معادلهای انگلیسی راحت ترم از طرفی این موارد رو هم عموما همه اطلاع دارن (خصوصا اگر کتب یا مقالات اصلی مطالعه بشن) برای همین زیاد وقت صرف نکردم تا معادلهای فارسی رو بنویسم یا به فرم اصلی (کاهلی ازبنده بود بخاطر مشغله زیاد) .representation به بازنمایی و یا بازنمود هم ترجمه میشه.
انشاءالله این تذکر صحیح شما رو در اسرع وقت طی ویرایشهای اینده ترتیب اثر میدم.
خیلی ممنونم بابت تذکر بجا
در پناه حق موفق و سربلند باشید
سلام
ممنون به خاطر اینکه زحمت کشیدید و این پست رو هم گذاشتید.
آقای مهندس در batch normalization در واقع هر کانال تصویر و یا هر فیچرمپ (در لایه های بعدی ) نسبت به میانگین و واریانس خود ش نرمالیزه میشه (البته در صورتی که نرمالیزه شدن به نفع عملکرد باشه که این مساله با اون دوتا پارامتر چک میشه)؟
یه سوال دیگه هم در مورد الگوریتم بهینه سازی GD_mini batch داشتم و اون اینکه، شبکه همزمان گرادیان رو برای هر نمونه بطور جداگانه محاسبه که کرد گرادیان نهایی رو میانگین میگیره بعد روی پارامترها تاثیر این میانگین گرادیان رو اعمال میکنه یا نه برای هر نمونه یک مجوعه فیلتر و پارامترهای سوا در نظر گرفته میشه و این مجموعه های مجزا هرکدام با گرادیان ناشی از خودشون فیدبک گرفته و آموزش داده میشن؟
می بخشید اگه سوال ها ابتدایی هست، چون من ساختار و معماری شبکه ها رو تا حدود زیادی خوب یاد گرفته ام اما متاسفانه هنوز ابهاماتی در مفاهیم مربوط به آموزش دارم.
ممنون از شما
سلام
در لایه کانولوشن هر فیچرمپ بطور جداگانه نرمال میشه و به همین خاطر هر کدوم یک مین و یک واریانس دارن (std, mean) نرمالسازی هم روی (batch_size * height * width) انجام میشه که نهایتا پارامترهای گاما و بتا رو به تعداد کانالها داشته باشیم.
در مورد سوال دوم هم میانگین در انتها محاسبه و بعد لحاظ میشه.
آموزش ماشین لرنینگ اندرو ان جی رو بخونید یا کتاب مارتین هاگان رو ببینید
سلام
ممنونم.
batch normalization در شبکه های lstm چجوری باید باشه؟آیا در ورودی همه لایه ها نیاز به نرمال سازی هست؟
سلام
متاسفانه تجربه کار با Lstm ها رو نداشتم تو سایت پرسش و پاسخ مطرح کنید عزیزانی که کار کردن راهنماییتون کنن.
با سلام
ببخشید منظورتون از اثر رگیولاریزیشن دقیقا چیه؟ با تشکر
سلام
معنی رگیولاریزیشن رو نمیدونید کلا یا اینجا چه اتفاقی می افته ؟
معنیش رو تو اصطلاح یادگیری ماشین نمی دونم چی هست؟
بعد ببخشید یک سوال ، وقتی ما در بچ نرمالیزیشن صحبت میکنیم، ما یک بار این عملیات را در لایه ی اول انجام می دهیم و وزن های خودمان رو نرمالایز می کنیم. در لایه بعدی که مجددا بچ نرمالیزشین داریم، وزن های لایه ی قبلی برای نرمالیزیشن لحاظ می شوند یا خیر؟ منظورم این هست که نرمالیزیشن فقط با داده ها یا همان وزنهای هر لایه صورت می گیرد یا وزن های لایه های پیشین هم در نرمالیزیشن لحاظ می شوند؟
سلام
بطور خیلی خلاصه رگیولاریزیشن فرایندی هست که در اون ما سعی میکنیم جلوی اورفیتینگ رو بگیریم
در بچ نرمالیزیشن در هر لایه ما عمل نرمالسازی رو داریم. نه ارتباطی با وزنهای لایه های قبلی نداره.
سلام
باتشکر. اگه میشه راجع به کارکرد لایه نرمالیزیشن در زمان تست هم اطلاعاتیو بدید؟
این لایه هم مثل دراپ اوت در زمان تست اعمال نمیشه؟
اگه میشه با مقادیر میانگین و واریانس داده های آموزش یا میانگین خود داده هاو و پارامترهای گاما و بتا چه مقداری دارن؟ مرسی
سلام در بچ نرمالیزیشن اینه که در زمان ترینینگ شما به مقادیر مناسب پارامترهایی مثل گاما و… برسید. زمانی که رسیدید
در زمان تست و ولیدیشن از اون مقادیر یادگرفته شده استفاده میشه. دقیقا مثل فیلترهای کانولوشن که در حین اموزش فراگرفته میشن و در زمان تست و ولیدیشن صرفا استفاده میشن. اینجا هم به همین شکله
سلام
خیلی عالی ولی کاش معادل های انگلیسی روهم میاوردین . اینکه فرمودین مقاله اصلی داخل کارگاه هست من باید از کجا به کارگاه دسترسی پیدا کنم؟
با تشکر
سلام.
مقاله اصلی این هست : https://arxiv.org/abs/1502.03167
تو سایت بگردید مطالب سال ۹۶ یا ۹۷ رو سرچ کنید پست مورد نظر رو میبینید از همونجا میتونید اسلاید و… رو دریافت کنید.
سلام
خیلی خوب بود، خدا خیرتون بده
واقعا ممنونم از توضیح بسیار جامع و کامل شما.
خیلی عالی بود. خیلی ممنون