مشکل محو شدگی گرادیان (vanishing gradient) در شبکه عصبی بازگشتی چیست؟

بسم الله الرحمن الرحیم

دراین نوشتار قصد داریم تا به یکی از مهمترین مشکلاتی که یک شبکه عصبی بازگشتی با آن مواجه است بپردازیم. در این بخش سعی ما بر این است که با مشکل محو شدگی گرادیان( و همینطور انفجار گرادیان) آشنا شده و  بطور مختصر به بیان راه حل های مقابله با آن بپردازیم.

تاریخچه!

دلیل محو شدگی گرادیان در شبکه عصبی بازگشتی چیست ؟

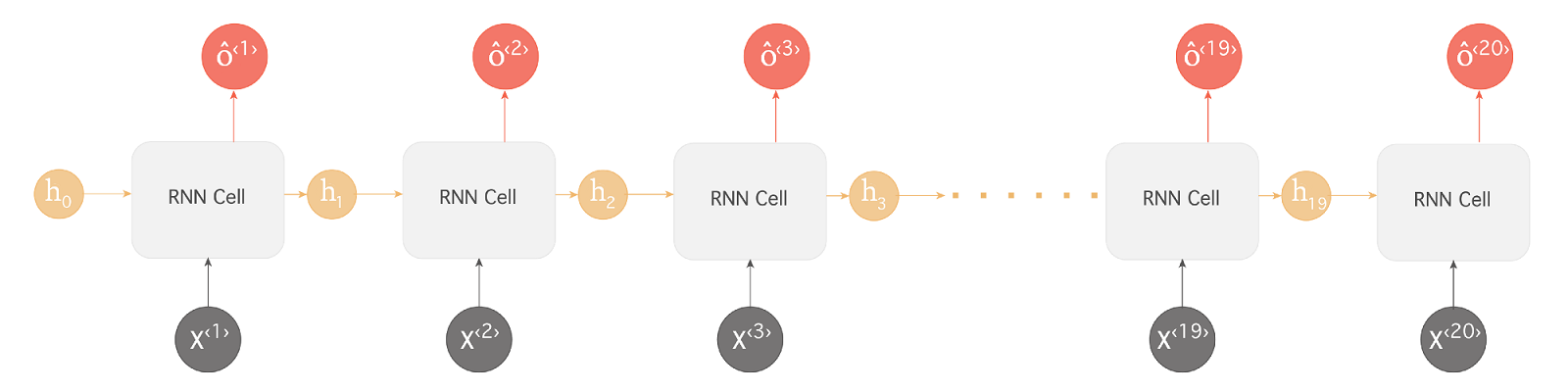
فرض کنید دنباله ورودی ما به شبکه جمله ای حاوی ۲۰ کلمه باشد ” دانش آموزان نخبه کشور ایران به مرحله نهایی المپیاد ریاضی رسیده … و به مقام نخست دست یافتند“

همانطور که در مثال بالا مشاهده میکنید شبکه عصبی بازگشتی ما برای اینکه بتواند کلمه “یافتند” را که در انتهای جمله آمده است بدرستی پیش بینی کند نیازمند اطلاعاتی از ابتدای جمله (کلمه دانش آموزان) است. به این نوع وابستگی ها وابستگی های بلند-مدت گفته میشود چرا که فاصله نسبتا قابل توجهی بین اطلاعات مرتبط (در اینجا دانش آموزان) و نقطه ای که این اطلاعات جهت انجام یک پیش بینی (یافتند) مورد استفاده است وجود دارد. متاسفانه در عمل هرچه این فاصله بیشتر شود شبکه های عصبی RNN با مشکل بیشتری در یادگیری این وابستگی ها مواجه میشوند چرا که یا با مشکل محو شدگی گرادیان یا انفجار گرادیان برخورد میکنند.

این مشکلات در حین آموزش یک شبکه عمیق در زمانی که گرادیان ها در فرایند پس انتشار از انتهای شبکه به سمت ابتدای شبکه منتقل میگردند رخ میدهد. گرادیان هایی که از لایه های انتهایی می آیند باید ضرب های متعددی را پشت سرگذاشته تا به لایه های ابتدایی برسند (بخاطر قائده زنجیره ای حسابان) و اینطور رفته رفته مقادیر آنها شروع به کوچک شدن میکند (کمتر از۱). این فرایند انقدر ادامه میابد و این مقادیر انقدر کوچک میشوند که (در شبکه های بسیار عمیق) فرآیند آموزش مختل شده و عملا متوقف میگردد چرا که گرادیان ها مقادیر بسیار ناچیزی داشته (محو شدگی گرادیان) که تاثیری در تغییر وزنها صورت نمیدهند. به این مشکل، مشکل محو شدگی گرادیان گفته میشود. به همین شکل امکان انفجار گرادیان نیز وجود دارد و مقادیر گرادیان رفته رفته انقدر بزرگ میشوند تا نهایتا مدل دچار خطا گردد (سرریز در محاسبات رخ دهد.(دریافت nan! در پایتون بعنوان مثال یکی از علائم این مساله است)

نکته

هرچقدر یک گرادیان کوچکتر باشد شبکه در بروزرسانی وزنها به مشکل بیشتری بر میخورد و مدت زمان بیشتری زمان میبرد تا به نتیجه نهایی برسد.

به عنوان مثال ۱۰۰۰ دوره ممکن است برای رسیدن به وزن ایده آل برای گام زمانی t کفایت کند اما برای آموزش وزنها برای گام های زمانی عقبتر مثل t-k (وقتی k<=t/2 باشد) بعلت کوچک بودن بیش از حد گرادیان در این گام ها ممکن است کافی نباشد. دقت کنید مشکل فقط این نیست که نیمی از شبکه بدرستی اموزش نمیبیند! بلکه مساله اینجاست که خروجی لایه های ابتدایی بعنوان ورودی برای لایه های بعدی مورد استفاده قرار میگیرند بنابر این اموزش در گام زمانی t و همینطور الی اخر وابسته به ورودی هایی است که از این لایه های (ابتدایی) اموزش ندیده بدست می آید. بنابر این بخاطر مشکل محو شدگی گرادیان کل شبکه بدرستی آموزش نخواهد دید.

پس اگر بخواهیم خلاصه کنیم اگر ما کوچک باشد ما با مشکل محو شدگی گرادیان مواجه هستیم و اگر این وزن بزرگ باشد ما با مشکل انفجار گرادیان مواجه خواهیم بود. در مساله محو شدگی گرادیان هرچه بیشتر از داخل شبکه عبور کنیم(در فاز پس انتشار) مقدار گرادیان ما کوچکتر شده و در نتیجه آموزش وزنها سخت تر میشود تا جایی که دیگر عملا اموزش متوقف میشود . دقت کنید این موضوع مانند یک دومینو بر روی تمامی وزنهای بعدی در سراسر شبکه اثر خواهد داشت.

چگونگی برخورد با انفجار گرادیان

زمانی که گرادیان ها اصطلاحا منفجر میشوند، اگردر حال استفاده از  از زبان پایتون باشیم عموما شاهد NaN خواهیم بود (بعلت رخ دادن سرریز در محاسبات. اگر این مساله در زمان استفاده از چارچوب های یادگیری عمیق مثل تنسورفلو یا پای تورچ و… دیده باشید یکی از دلایل محتمل میتواند همین قضیه باشد) و یا ممکن است شاهد تناوب های نامنظم  مقادیر Loss بدست امده در حین آموزش شبکه باشیم. راه حل های مختلفی در طی سالیان اخیر برای مقابله با این مشکل در شبکه های عصبی بازگشتی ارائه شده است. از آن جمله میتوان به استفاده از L1/L2 weigh decay , پیش اموزش مدل، teacher forcing و…اشاره کرد. راه دیگری که پیشنهاد میشود این است که عملیات پس انتشار را تا یک گام زمانی معین انجام دهیم که معمولا بهینه نیست چرا که همه وزنها در این حالت بروز نمیشوند. اما برای این مساله عموما همیشه یکی از روشهای پیشنهادی gradient clipping است.

روش gradient clipping اولین بار در مقاله ای تحت عنوان ” On the difficulty of training recurrent neural networks” در سال ۲۰۱۳ معرفی گردید و بطور ساده روشی جهت مقابله با محو شدگی و انفجار گرادیان است. در این روش مقادیر گرادیان نسبت به یک حد آستانه مقایسه شده و اینگونه از افزایش و یا کاهش بی رویه مقدار آن جلوگیری شود. با استفاده از این آستانه گیری جهت گرادیان ثابت مانده و تنها بزرگی عددی آن محدود میشود.

که در عبارت بالا g گرادیان و نیز norm آن میباشد.

در زیر شمایلی از وضعیت گرادیان ها در بستر خطا قبل و بعد از اعمال روش gradient clipping را مشاهده میکنید (منبع کتاب deeplearning اثر ایان گود فیلو انتشارات MIT )

نکته :

برای مقابله با مشکل vanishing gradient یکی از موثرترین راه ها استفاده از مقداردهی اولیه مناسب وزن هاست که یکی از معروف ترین الگوریتم ها برای این منظورالگوریتم مقداردهی اولیه Xavier است.

مقابله با مشکل محو شدگی گرادیان:

برای مشکل محو شدگی گرادیان راه های مختلفی ارائه شده است. یک راه عدم استفاده از الگوریتم های یادگیری مبتنی بر گرادیان کاهشی است! روش Hessian Free Optimizer With Structural Dumping یکی از این روشهاست که از ماتریس Hessian  بهره میبرد. یک راه حل ساده جهت مقابله با مشکل گرادیان محو شونده استفاده از معماری شبکه عصبی بازگشتی همانی(Identity RNN) است . در این شبکه وزنها همگی بر اساس ماتریس همانی مقداردهی اولیه شده و بجای tanh از تابع فعالسازی ReLU استفاده میشود. این عمل سبب میشود تا محاسبات شبکه نزدیک به تابع همانی بوده و به همین دلیل نیز مشتق خطا که در زمان پس انتشار منتقل میشود همیشه مقداری برابر با ۰ یا ۱ خواهد داشت بنابر این با مشکل محو شدگی گرادیان مواجه نخواهیم بود.

راه حل دیگری که عموما به بخش جدایی ناپذیری از شبکه های عصبی عمیق (چه شبکه های پیش خور همانند CNN و MLP و چه شبکه های عصبی بازگشتی همانند RNN )تبدیل شده است استفاده از مقداردهی مناسب وزنهاست بگونه ای که پتانسیل رخداد محو شدگی گرادیان کمینه شود. به این منظور امروزه از الگوریتم های مقداردهی اولیه ای نظیر Xavier و یا  MSRA (که به He initialization یا Kaiming initialization هم معروف است) برای این کار استفاده میشود.
راه حل دیگری که بطور گسترده مورد استفاده قرار میگیرد استفاده از معماری LSTM است . LSTM گونه دیگری از شبکه عصبی بازگشتی است که بطور ویژه بگونه ای طراحی شده است تا وابستگی های زمانی بلند مدت در دنباله ورودی را دریافت و حفظ کند. این شبکه عصبی بازگشتی بگونه ای عمل میکند که مقادیر حالت مخفی توسط سایر مقادیر فعالسازی محلی که نزدیک به آنهاست تحت تاثیر قرار میگیرند که این قابلیت نقش حافظه کوتاه مدت را بازی میکند درحالی که وزن های شبکه توسط محاسباتی که بر روی تمام دنباله رخ میدهد تاثیر میپذیرند که این به منزله حافظه بلند مدت است. بنابر این نوع از شبکه ها بگونه ای طراحی شده اند که در آن مقادیر فعالسازی حالت مخفی آن بتوانند همانند وزن ها عمل کرده و اطلاعات را در فاصله های زیاد حفظ کنند. به همین علت این نوع از شبکه ها به شبکه های حافظه کوتاه و بلند مدت معروف شده اند.

منابع جهت مطالعه بیشتربصورت لینک در متن آموزش قرار داده شده اند و به مرور مباحث این بخش تکمیل تر میشود.