آموزش شبکه کانولوشن بخش دوم

بسم الله الرحمن الرحیم

این بخش دوم آموزش شبکه های کانولوشن هست . تصاویر زیادی این اموزش داره خصوصا اخر و یکسری از فرمول ها رو هم مجبور شدم از word عکس بگیرم. حواستون باشه که اگه جایی چیزی باید باشه و نیست بدونید عکس لود نشده! انشاالله سرفرصت داکیومنت این هم برای دانلود قرار میدم.

لایه Convolutional

لایه کانولوشن هسته اصلی تشکیل دهنده شبکه عصبی کانولوشن است, و توده خروجی آن را میتوان بصورت یک توده سه بعدی از نورون ها تفسیر کرد. به زبان ساده تر یعنی اینکه خروجی این لایه یک توده سه بعدی است . برای درک بهتر این مسئله شبکه های عصبی معمولی را در نظر بگیرید . در شبکه های عصبی معمولی هر لایه چیزی جز لیستی(یک بعدی همانند یک مستطیل!) از نورون ها نبود که هر نورون خروجی خاص خود را تولید میکرد و نهایتا یک لیست از خروجی ها که متناظر با هر نورون بود حاصل میشد . اما در شبکه عصبی کانولوشن بجای یک لیست ساده ما با یک لیست سه بعدی (یک مکعب !) مواجه هستیم که نورونها در سه بعد آن مرتب شده اند. در نتیجه خروجی این مکعب نیز یک توده سه بعدی خواهد بود . تصاویر زیر این مفهوم و تفاوت بین این دو مفهوم را بهتر بیان میکند .

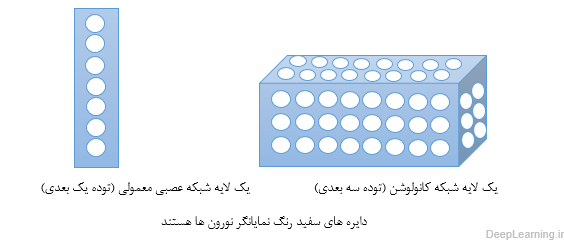
در اینجا ما در مورد جزییات اتصالات نورون ها و نحوه قرارگیری آنها در فضا و طرح اشتراک پارامتر آنها صحبت میکنیم .

خلاصه و درک شهودی مسئله :

پارامترهای لایه کانولوشن شامل مجموعه ای از فیلترهای قابل یادگیری هستند. هر فیلتر از لحاظ مکانی کوچک بوده [۱] اما در امتداد عمق توده ورودی ادامه پیدا میکند. به زبان ساده تر میتوان اینطور گفت که ما با یک توده سه بعدی مواجه هستیم . این توده سه بعدی دارای یک طول و عرض و یک عمق است. اگر فرض کنیم عمق ما برابر با x باشد به این معناست که ما x برش (قاچ) از توده خواهیم داشت. بعنوان مثال اگر عمق برابر با ۱ باشد ما با یک ماتریس ساده (آرایه دوبعدی) مواجه هستیم که دارای طول و عرض است . حال اگر عمق برابر با ۲ باشد یعنی ما دارای دو ماتریس هستیم . یعنی در هر عمق در اصل یک ماتریس وجود دارد. بنابر این زمانی که ما میگوییم فیلتر مورد نظر در امتداد یا راستای عمق ادامه میابد به این معناست که این فیلتر بر روی تمامی ماتریس ها (برش های توده ورودی ) اعمال میشود.

یک توده سه بعدی با عمق برابر با ۲ که بصورت عمودی برش داده شده است .

در زمان forward pass ما هر فیلتر را در امتداد پهنا (width) و ارتفاع (height) ورودی میلغزانیم (در اصل convolve میکنیم ) با این کار ما یک نگاشت فعال سازی(Activation Map) دو بعدی برای آن فیلتر ایجاد میکنیم. همانطور که ما فیلتر را در عرض ورودی میلغزانیم (slide میدهیم) ضرب نقطه ای بین ورودی های فیلتر با ورودی را هم انجام میدهیم . بصورت شهودی, شبکه, فیلترهایی که در زمان مشاهده برخی از ویژگی های خاص در بعضی موقعیتهای مکانی در ورودی فعال میشوند را یاد میگیرد . با انباشته کردن این نگاشتهای فعال سازی (Activation Maps) برای تمامی فیلترها در راستای بُعد عمق ,توده خروجی کامل بدست می آید . هر مدخل در این توده خروجی را میتوان بعنوان خروجی یک نورون که تنها به ناحیه کوچکی در ورودی نگاه میکند در نظر گرفت که پارامترهای مشترک با بقیه نورون ها در همان نگاشت فعال سازی (Activation Map)دارد(چرا که این اعداد همه نتیجه اعمال یک فیلتر یکسان هستند ).

اتصال محلی (Local Connectivity):

زمانی که ما با ورودی هایی با ابعاد بالا(high dimensional) مثل تصاویر مواجه هستیم[۲], همانطور که در بالا دیدیم اتصال نورون ها به تمام نورونهای قبل از خود (در توده قبلی) غیر عملی است. بنابر این بجای اینکار ما هر نورون را تنها به ناحیه کوچکی از توده ورودی متصل میکنیم .میزان وسعت این ناحیه کوچک برای اتصال یک فراپارامتر است که به آن receptive field و یا ناحیه ادراکی گفته میشود . وسعت اتصال در محور عمق همیشه مساوی با عمق توده ورودی است .توجه به این عدم تقارن در نحوه برخورد ما با ابعاد مکانی (طول و عرض تصویر و یا همان عرض و ارتفاع ) و بعد عمق حائز اهمیت است. ارتباطات در مکان محلی هستند یعنی در راستای عرض و ارتفاع تصویر هستند اما همیشه تمام عمق توده ورودی را در بر میگیرند. اجازه دهید با یک مثال توضیح بیشتری بدهیم . فرض کنید توده ورودی ما دارای اندازه ای برابر با ۳x32x32 باشد ( مثلا یک عکس رنگی (RGB) از دیتاست CIFAR-10 ). حال اگر ناحیه ادراکی (Receptive Field) اندازه ای برابر با ۵×۵ داشته باشد این به این معناست که هر نورون در لایه کانولوشن برای ناحیه ای در توده ورودی با اندازه ۵x5x3 تعداد وزنی برابر۵x5x3=75 خواهد داشت. لطفاً دقت کنید که میزان وسعت اتصال در امتداد محور عمق باید مساوی ۳ باشد چرا که عمق توده ورودی ما ۳ است ( تصویر ورودی ما دارای ۳ کانال رنگ است). پس همانطور که دقت کردید اتصالات فقط در راستای عرض و ارتفاع تصویر ورودی نیستند بلکه در محور عمق هم امتداد پیدا میکنند. و این به زبان ساده تر به این معناست که اگر تصویر رنگی ورودی خود با ۳ کانال رنگ را ۳ ماتریس که پشت سر هم قرار گرفته اند در نظر بگیریم . توضیحات بالا به این معناست که ما ناحیه ای به اندازه ۵×۵ را بر روی تمام این سه ماتریس اعمال میکنیم . تصویر زیر این مطلب را بهتر نشان میدهد.

نمایشی از ارتباط در یک توده که در راستای عرض و ارتفاع در امتداد عمق ادامه یافته است

مثال دوم را در نظر بگیرد. فرض کنید توده ورودی اندازه ای برابر با ۱۶x16x20 داشته باشد. بنابر این با استفاده از ناحیه ادراکی (Receptive field) با اندازه ۳×۳ هر نورون در لایه کانولوشن تعداد ۳x3x20 = 180 اتصال به توده ورودی خواهد داشت. توجه کنید که اتصال در فضا محلی است ( مثلا در اینجا ۳×۳ است ) اما تمام عمق را در بر گرفته است (۲۰)

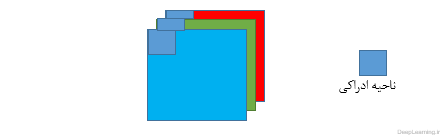
تصویر سمت چپ یک توده ورودی را نشان میدهد که با رنگ قرمز مشخص شده است ( مثلا یک عکس با اندازه ۳x32x32 از دیتا ست CIFAR-10). همینطور شما میتوانید یک توده از نورون ها را در لایه کانولوشن که به رنگ آبی نمایش داده شده است مشاهده کنید. هر نورون در لایه کانولوشن تنها به یک ناحیه محلی از لحاظ مختصات مکانی( طول و عرض) در توده ورودی متصل است اما این ارتباط در عمق بصورت کامل امتداد میابد(یعنی تمام کانال های رنگ را در بر میگیرد).توجه کنید که چندین نورون ( در این مثال ۵ نورون ) در راستای عمق وجود دارند که همگی به یک ناحیه در ورودی نگاه میکنند(توضیحات ببیشتر در ادامه داده میشود).

تصویر سمت راست ساختار یک نورون را نشان میدهد که دقیقا همانند چیزی است که در شبکه های عصبی معمولی مورد استفاده قرار میگیرد بعبارت دیگر نورون ها هیچ تفاوتی نسبت به قبل نکرده اند. آنها هنوز ضرب نقطه ای بین وزنها و ورودی ها را انجام داده و نتیجه را از یک تابع غیرخطی عبور میدهند و خروجی را تولید میکنند. تنها تفاوت در اینجا این است که اتصال دستخوش محدودیت شده است به این معنا که اتصالات آنها باید از لحاظ مکانی محلی باشد

ما تا به اینجا در مورد اتصال هر نورون به توده ورودی در لایه کانولوشن صحبت کردیم اما چیزی در مورد اینکه چه تعداد نورون در توده خروجی بایستی وجود داشته باشند و یا اینکه ترتیب قرار گیری آنها به چه صورت باید باشد صحبتی نکردیم.۳ فراپارامتر (Hyper parameter) اندازه توده خروجی را کنترل میکنند. این سه پارامتر عمق (depth) ,گام (stride) و لایه گذاری با صفر (zero-padding) هستند. در زیر به توضیح بیشتر این پارامترها میپردازیم.

عمق توده خروجی پارامتری است که ما میتوانیم خود انتخاب کنیم . این پارامتر تعداد نورون هایی که در لایه کانولوشن به یک ناحیه در توده ورودی متصل میشوند را کنترل میکند. این پارامتر همانند حالتی در شبکه های عصبی معمولی است که ما در یک لایه مخفی چندین نورون داشتیم که همه به یک ورودی متصل بودند. همانطور که جلوتر خواهیم دید تمام این نورون ها یاد میگیرند که برای ویژگی های مختلف موجود در ورودی فعال شوند. بعنوان مثال اگر لایه کانولوشن اول یک تصویر خام را بعنوان ورودی دریافت کند, نورون هایی که در امتداد بعد عمق قرار دارند ممکن است با مواجهه با لبه های جهتدار (oriented edges) و یا لکه های رنگ (blobs of color) فعال شوند. ما به مجموعه نورون هایی که همه به یک ناحیه یکسان از ورودی نگاه میکنند یک ستون عمقی یا depth column میگوییم.

ما باید گام (stride) را که بوسیله آن ستون های عمقی (depth column) را حول ابعاد مکانی (عرض و ارتفاع) معین میکنیم مشخص کنیم. زمانی که stride برابر با ۱ باشد ما یک ستون عمقی (depth column) جدید از نورون ها را به مختصات مکانی با فاصله تنها ۱ واحد مکانی از هم, اختصاص میدهیم. این باعث بوجود آمدن نواحی ادراکی دارای اشتراک زیاد بین ستونها و همچنین توده های خروجی بزرگ میشود. برعکس اگر ما گام ها (stride) را بزرگتر بگیریم نواحی ادراکی اشتراک کمتری داشته و توده خروجی نیز از لحاظ ابعاد مکانی کوچکتر میشود.

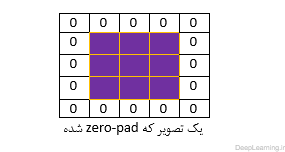
همانطور که بزودی خواهیم دید بعضی اوقات راحت تر است که مرز توده ورودی را با صفر بپوشانید(zero-pad) . به عبارت دیگر یعنی دور تصویر ورودی را با صفر پر کنیم . مثل اینکه یک سطر ۰ و یک ستون ۰ به ابتدا و انتهای تصویر اضافه کنیم اینطور تصویر ما در داخل قابی از صفر قرار خواهد گرفت مثل شکل زیر:

اندازه این Zero-padding یک فراپارامتر(hyper parameter) است . ویژگی خوب این پارامتر این است که بما اجازه کنترل کردن اندازه توده خروجی را میدهد. بطور خاص ما بعضی اوقات میخواهیم که دقیقا اندازه مکانی توده ورودی حفظ شود.

ما برای محاسبه اندازه (مکانی) توده خروجی میتوانیم از اندازه توده ورودی (W) اندازه ناحیه ادراکی نورون های لایه کانولوشن (F) , اندازه گام (stride) و مقدار zero padding که روی مرزهای توده ورودی اعمال شده استفاده کنیم . ما میتوانیم از فرمول: برای محاسبه اینکه چه تعداد نورون مناسب است استفاده کنیم (با تست این فرمول میتوانید به درستی آن پی ببرید) اگر نتیجه این فرمول یک عدد اعشاری باشد این به این معناست که مقدار استفاده شده برای stride نادرست بوده و نورون ها را نمیتوان با این مقدار طوری کنار یکدیگر مرتب کرد که بخوبی در سرتاسر توده ورودی بصورت متقارن جای شوند. برای درک این فرمول مثال زیر را در نظر بگیرید .

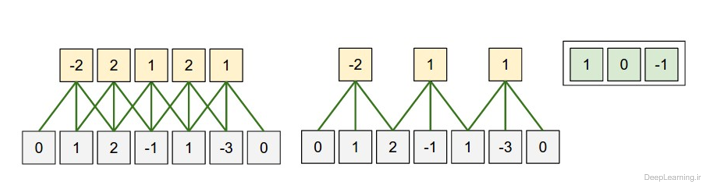
تصویری از ترتیب (قرارگیری) مکانی.

در این مثال تنها یک بعد مکانی (محور x) , یک نورون با ناحیه ادراکی با اندازه F = 3 و یک ورودی با اندازه W = 5 وجود دارد(۱,۲,-۱,۱,-۳). Zero padding هم برابر با P = 1 است. (یک صفر به دو طرف ورودی اضافه شده است)
در تصویر سمت چپ stride با اندازه S = 1 اعمال شده است که باعث اندازه خروجی : شده است. در تصویر سمت راست stride با اندازه S = 2 باعث اندازه خروجی :شده است. توجه کنید که stride با اندازه S = 3 امکان پذیر نمیباشد چرا که با این مقدار نمیتوان نورون ها را بخوبی در سرتاسر توده جای داد. اگر از لحاظ فرمولی بخواهیم به این مسئله نگاه کنیم میبینیم که مقدار ۴=۲+۳-۵ بر ۳ قابل تقسیم نیست (بخش پذیر نیست). وزن نورونها در این مثال [۱,۰,-۱] (همانطور که در منتها الیه تصویر سمت راست نمایش داده شده است ) و بایاس آن برابر با ۰ میباشد.. این وزنها بین تمام نورون های زرد رنگ مشترک است (بخش اشتراک پارامترها را در زیر بخوانید)

استفاده از Zero-padding :

در مثال قبل (تصویر سمت چپ) توجه کنید که بُعد ورودی برابر ۵ و بعد خروجی نیز مساوی ۵ بود. به این خاطر این اتفاق رخ داد چرا که ناحیه ادراکی برابر با ۳ بود و ما از zero padding مساوی با ۱ استفاده کردیم . اگر zero padding یی وجود نداشت , توده خروجی تنها بعدی برابر با ۳ میداشت. چرا که تنها این تعداد نورون در سرتاسر ورودی اصلی میتوانستند جا بگیرند. بطور کلی تنظیم مقدار Zero padding بر اساس فرمول:در زمانی که Stride برابر با S = 1 باشد اطمینان حاصل میکند که توده ورودی و توده خروجی هر دو از لحاظ مکانی دارای اندازه یکسانی خواهند بود. استفاده از Zero padding به اینصورت بسیار رایج بوده و ما توضیحات تکمیلی را جلوتر زمانی که در مورد معماری شبکه های کانولوشن بیشتر صحبت میکنیم خواهیم داد.

محدودیت های Stride

توجه کنید که ترتیب مکانی فراپارامترها (Hyper paramters) محدودیت های دوطرفه دارند. بعنوان مثال زمانی که اندازه ورودی برابر با ۱۰ بوده و هیچ zero padding استفاده نشده باشد (P=0) و اندازه فیلتر برابر با F=3 باشد بنابر این استفاده از stride یی با اندازه S = 2 غیر ممکن خواهد بود. چرا که: که همانطور که مشاهده میکنید نتیجه یک عدد صحیح نبوده و فلذا نورون ها نمیتوانند بصورت متقارن و بخوبی در سرتاسر ورودی جای(قرار) بگیرند. بنابراین این مقادیر این فراپارامترها نامعتبر در نظر گرفته میشود و اگر شما سعی کنید یک شبکه عصبی کانولوشن با این مقادیر در یک کتابخانه مربوط به شبکه عصبی کانولوشن ایجاد کنید به احتمال بسیار زیاد با یک Exception مواجه خواهید شد. همانطور که جلوتر در بخش معماری های شبکه کانولوشن خواهیم دید, تنظیم اندازه ها در شبکه کانولوشن بصورت مناسب بطوری که تمامی ابعاد آن بدرستی کار کنند کار واقعا طاقت فرسایی میتواند باشد که البته با استفاده از Zero-padding و تعداد دیگری از راهکارهای طراحی تا حد بسیار زیادی میتوان از سختی آن کاهید.

[۱] یعنی تنها بخشی از عرض و ارتفاع را شامل میشود. (مثلا اگر عرض و ارتفاع تصویر به ترتیب برابر ۳۲ و ۳۲ باشد. فیلتر ممکن است اندازه برابر با ۴×۴ داشته باشد.

[۲] به متغیرهای مختلف که در نتیجه مسئله ای دخیل هستند در Machine learning بُعد گفته میشود. در اینجا هر پیکسل یک تصویر یک متغییر بحساب می آید (چرا که بصورت یک ورودی مجزا به شبکه ارائه میشود و مقدار آن در کارکرد شبکه موثر است ) . بنابر این یک تصویر با ۲۰x20x3 1200 بعد خواهد داشت. از این رو در اینجا ابعاد بالای تصاویر به معنای بزرگتر بودن اندازه تصاویر است.

نمونه واقعی از شبکه های عصبی کانولوشن

معماری Krizhevsky et al که برنده رقابت ImageNet در سال ۲۰۱۲ شد تصاویری با اندازه ۲۲۷x227x3 را بعنوان ورودی دریافت میکرد. در لایه کانولوشن اول این شبکه از نورون هایی با ناحیه ادراکی با اندازه F=11 , Stride با مقدار S=4 و zero padding P = 0 استفاده میشد. از آنجایی که ۵۵=۱+۴/(۱۱-۲۲۷) و عمق لایه کانولوشن برابر با K = 96 بود توده خروجی لایه کانولوشن اندازه ای برابر با ۵۵x55x96 داشت. هر کدام از ۵۵x55x96 نورون در این توده به ناحیه ای از ورودی با اندازه ۱۱x11x3 متصل بودند. علاوه بر آن تمام ۹۶ نورون در هر ستون عمقی (depth column) هم به یک ناحیه از ورودی با اندازه ۱۱x11x3 متصل بودند البته با وزنهای متفاوت.

اشتراک پارامتر

طرح اشتراک پارامتر در لایه های کانولوشن به منظور کنترل تعداد پارامترها مورد استفاده قرار گرفت. با استفاده از نمونه عینی که در بالا داده شد, ما میبینیم که ۵۵x55x96=290,400 نورون در لایه کانولوشن اول وجود دارد و هر کدام از آنها ۱۱x11x3=363 وزن و ۱ بایاس دارند. همه اینها با هم تشکیل ۲۹۰۴۰۰×۳۶۴=۱۰۵,۷۰۵,۶۰۰ پارامتر را تنها برای لایه اول شبکه کانولوشن میدهند. کاملا پیداست که این عدد بسیار بزرگی است.

ما میتوانیم با یک فرض منطقی تعداد بسیار زیادی ازاین پارامترها را کاهش دهیم. و آن فرض این است که اگر یک Patch feature برای محاسبه در یک موقعیت مکانی (x,y) مفید باشد پس باید برای محاسبه همان feature در موقعیت متفاوت (x2,y2) هم مفید باشد. به عبارت دیگر اگر یک برش دو بعدی از عمق را یک برش عمقی بنامیم (بعنوان مثال یک توده با اندازه ۵۵x55x96 دارای ۹۶ برش عمقی است که هر کدام دارای اندازه ۵۵×۵۵ میباشند) ما هر نورون در این برش عمقی را محدود به استفاده از یک مجموعه وزن و بایاس میکنیم . با این طرح اشتراک پارامتر, لایه کانولوشن اول در مثال ما حالا فقط ۹۶ مجموعه وزن یکتا خواهد داشت (یک مجموعه وزن برای هر برش عمقی ) که در کل برابر ۹۶x11x11x3 = 34,848 وزن یکتا یا ۳۴,۹۴۴ پارامتر (به اضافه ۹۶ بایاس) خواهد بود . متناوبا تمام ۵۵×۵۵ نورون موجود در هر برش عمقی حالا از یک مجموعه پارامتر استفاده میکنند. در عمل در حین Backpropagation هر نورون موجود در توده gradient را برای وزنهایش حساب میکند اما این gradient ها درسرتاسر هر برش عمقی جمع شده و تنها یک مجموعه وزن در هر برش را بروز میکند.

توجه کنید که اگر تمام نورون ها در یک برش عمقی از یک بردار وزن یکسان استفاده کنند بنابر این عملیات forward pass لایه کانولوشن میتواند در هر برش عمقی بصورت ضرب (convolution) بین وزنهای نورون با توده ورودی محاسبه شود (برای همین به آن لایه کانولوشن گفته میشود) بنابر این رایج است که به مجموعه وزن ها بعنوان یک فیلتر نگاه شود( یا یک کرنل). که با ورودی ضرب (convolve) شده است. نتیجه این عمل (Convolution) یک نگاشت فعالسازی (Activation map) است ( مثلا با اندازه ۵۵×۵۵ ) و مجموعه این Activation map ها برای هر فیلتر مختلف در راستای بعد عمق بر روی هم قرار گرفته تا توده خروجی را ایجاد کنند(مثلا با اندازه ۵۵x55x96)

فیلترهای نمونه که توسط Krizhevsky et al یادگرفته شده اند. هر کدام از این ۹۶ فیلتر نمایش داده شده در اینجا اندازه ای برابر با ۱۱x11x3 دارند و هر کدام از انها با ۵۵×۵۵ نورون در یک برش عمقی به اشتراک گذاشته شده اند. دقت کنید که فرض اشتراک پارامترها نسبتا منطقی هم هست. اگر کشف یک لبه افقی در جایی از تصویر مهم باشد, قائدتا برای سایر مکانها در تصویر هم باید بواسطه ساختار translationally-invariant تصاویر مفید باشد. بنابر این دیگر نیازی به یادگیری دوباره کشف لبه افقی برای تک تک ۵۵×۵۵ مکان مشخص در توده خروجی لایه کانولوشن نیست. یعنی لازم نیست تا این عمل یادگیری کشف لبه افقی برای تک تک مکان ها تکرار شود.

توجه کنید که بعضی اوقات فرض اشتراک پارامتر ممکن است منطقی بنظر نیاید. خصوصا زمانی که تصاویر ورودی به یک شبکه کانولوشن دارای ساختارهای وسط چین (specific centered structure) خاص باشند, که ما باید انتظار داشته باشیم , بعنوان مثال ویژگی های مختلفی از یک طرف تصویر نسبت به طرف دیگر یاد گرفته شود. یک نمونه عملی از این مورد زمانی است که تصاویر صورت وسط چین شده اند. ممکن است ما انتظار داشته باشیم که ویژگی های مختلف مخصوص مو (hair specific) و یا مخصوص چشم (eye-specific) بتوانند ( و باید) در موقعیتهای مکانی مختلف یاد گرفته شوند. در این حالت معمولا رایج است که طرح اشتراک پارامتر را کنار گذاشته و بجای آن خیلی ساده به آن لایه بصورت محلی متصل (Locally connected layer)گفته شود.

برای اینکه مطالبی که تا بحال بیان شد را بهتر درک کنیم در اینجا سعی میکنیم مفاهیم بیان شده را در قالب کد بیان کنیم . برای اینکار از زبان پایتون استفاده میکنیم که امروزه یکی از زبانهای بسیار پرکاربرد خصوصا در زمینه Deep learning و شبکه های کانولوشن است.

ما برای راحتی هرچه بیشتر از کتابخانه Numpy استفاده میکنیم که یکی از کتابخانه های مشهور پایتون در زمینه کار با عملیاتهای برداری است.سینتکس این کتابخانه هم شبیه به متلب بوده و کسانی که با متلب آشنایی دارند براحتی دستورات معادل را درک میکنند.

فرض کنید توده ورودی ما یک آرایه با نام X باشد. در اینصورت :

• برای بدست آوردن یک depth column در موقعیت (x,y) از دستور X [ x , y , : ] استفاده میکنیم
• برای بدست آوردن یک برش عمقی (depth slice) یا بطور مساوی همان نگاشت فعال سازی(activation map) در عمق d از دستور X[ : , : , d ] استفاده میکنیم.

فرض کنید توده ورودی X دارای ابعاد X.shape: (11,11,4) باشد این دستور یعنی توده ای با اندازه ۱۱x11x4 ایجاد شود که به معنای عرض و ارتفاع ۱۱ و عمق ۴ میباشد. حال فرض کنید ما از Zero padding استفاده نکنیم ( یعنی P=0 ) و اندازه فیلتر (یا همان ناحیه ادراکی ) برابر با F = 5 و stride هم برابر S = 2 باشد. با توجه به این اطلاعات ما میتوانیم اندازه مکانی (یعنی عرض و ارتفاع) توده خروجی را بدست بیاوریم . اندازه توده خروجی برابر ۴=۱+۲/(۵-۱۱) خواهد بود که به معنای توده ای با عرض و ارتفاع ۴ است . نگاشت فعال سازی (Activation map) نیز در توده خروجی (که از این به بعد به آن V میگوییم ) بصورت زیر خواهد بود ( دقت کنید ما تنها بعضی از محاسبات را در مثال زیر قید میکنیم)

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

ذکر این نکته ضروری است که در numpy عملیات ضرب (*) که در بالا شاهد آن هستید عمل ضرب خانه به خانه (elementwise) را در آرایه انجام میدهد. نکته دیگر آنکه بردار وزن W0 بردار وزن مربوط به نورون ۰ بوده و b0 هم بایاس مربوط به آن میباشد. در اینجا فرض کردیم W0 ابعادی بصورت ۵x5x4 دارد . (W0.shape: (5,5,4) ) , چرا که اندازه فیلتر (یا همان ناحیه ادراکی) برابر با ۵ بوده و عمق توده ورودی نیز برابر با ۴ است. توجه کنید که در اینجا ما همانند شبکه های عصبی معمولی ضرب نقطه ای را انجام میدهیم. همچنین در اینجا مشاهده میکنید که ما در حال استفاده از یک وزن و بایاس هستیم (بواسطه اشتراک پارامتر) و ابعاد در راستای عرض در گام های ۲ تایی (مقدار Stride) افزایش پیدا میکنند. به منظور ساختن نگاشت فعال سازی(Activation map) دوم در توده خروجی بصورت زیر عمل میکنیم :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1

نمونه ای از حرکت در راستای y:

• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1

نمونه ای از حرکت در هر دو راستای x وy:

• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1

جایی که مشاهده میکنید ما در حال اندیس گذاری در بُعد عمقی دوم در V (اندیس ۱ ) هستیم به این خاطر است که ما در حال محاسبه نگاشت فعال سازی دوم (Activation map) هستیم و به همین دلیل مجموعه متفاوتی از پارامترها (W1) باید استفاده شود. در مثال بالا ما بخاطر خلاصه سازی از نوشتن تمامی عملیات هایی که در لایه کانولوشن برای پر کردن باقی بخش های آرایه خروجی V صورت میگیرد پرهیز کردیم. علاوه بر آن بیاد داشته باشید که این نگاشتهای فعال سازی (Activation maps) اغلب بصورت خانه به خانه توسط یک تابع فعال سازی مثل ReLU مورد پردازش قرار میگیرند (تا خروجی نهایی تشکیل شود) اما این مسئله در اینجا نشان داده نشده است.

خلاصه

در اینجا ما بصورت خلاصه مطالبی که در بالا به آن پرداختیم را مرور میکنیم

یک شبکه کانولوشن :

یک توده با اندازه W₁ x H₁ x D₁ را بعنوان ورودی دریافت میکند که W نشانگر عرض , H نشانگر ارتفاع و D نشانگر عمق آن میباشد.

نیازمند ۴ فراپارامتر(Hyper parameter) است :

• تعداد فیلتر ها K
• اندازه وسعت مکانی(اندازه x , y) فیلترها )اندازه ناحیه ادراکی) F
• اندازه گام یا Stride S
• مقدار Zero padding P

تولید یک توده خروجی با اندازه W₂ x H₂ x D₂ که :

• W2=(W1-F+2P)/S+1
• H2=(H1-F+2P)/S+1 (یعنی عرض و ارتفاع هر دو بطور مساوی بصورت متقارن محاسبه میشوند)
• D2=K

با اشتراک پارامتر, دارای F.F.D₁ وزن به ازای هر فیلتر بوده که در کل F.F.D1).K) وزن و K بایاس میباشد.

برش dام ( با اندازه W2 X H2 ) ,در توده خروجی نتیجه انجام یک ضرب (convolution) معتبر بین فیلتر dام با توده ورودی با stride S بوده که سپس با بایاس d ام جمع شده است.

یک نمونه از مقادیر رایج برای فراپارامترهای توضیح داده شده در بالا بصورت F=3,S=1,P=1 است. البته شیوه ها و قوانین متداولی وجود دارند که باعث رسیدن به این مقادیر میشوند. (بخش معماری شبکه کانولوشن را برای اطلاعات بیشتر ببینید)

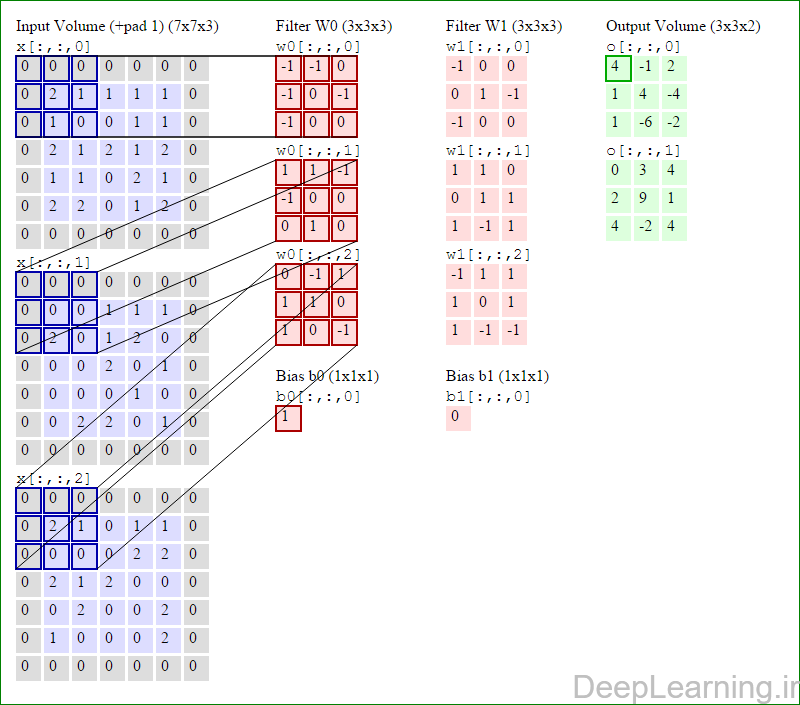
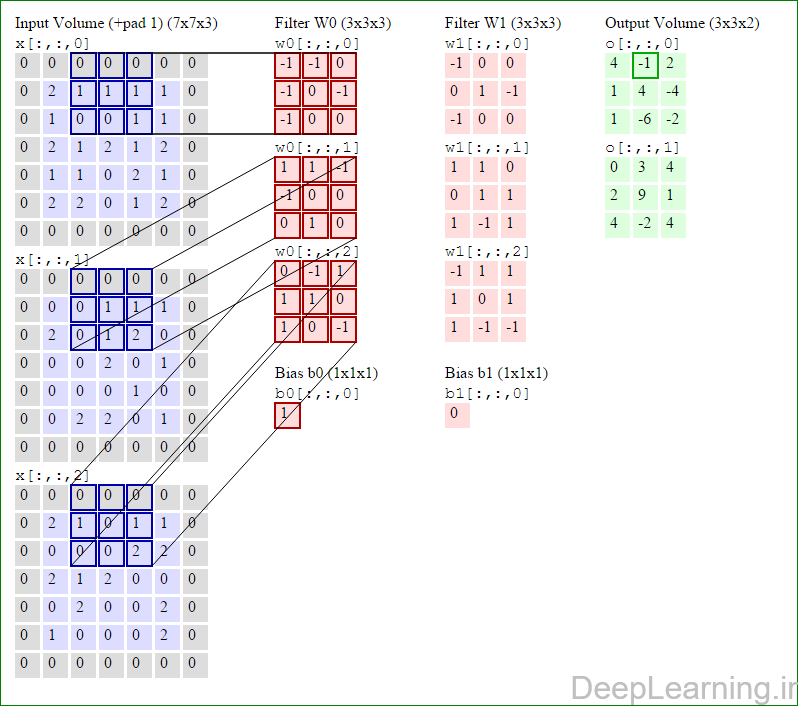
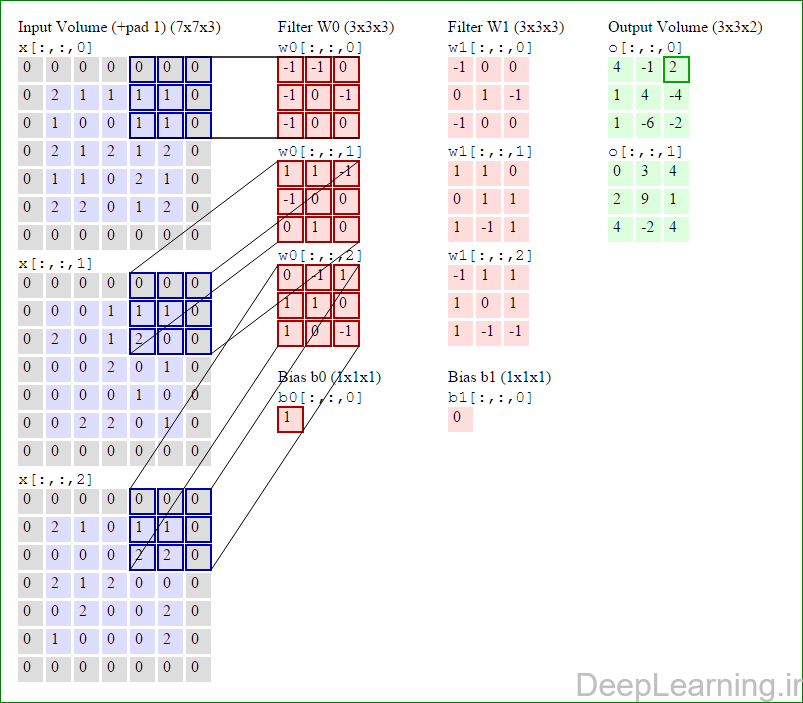
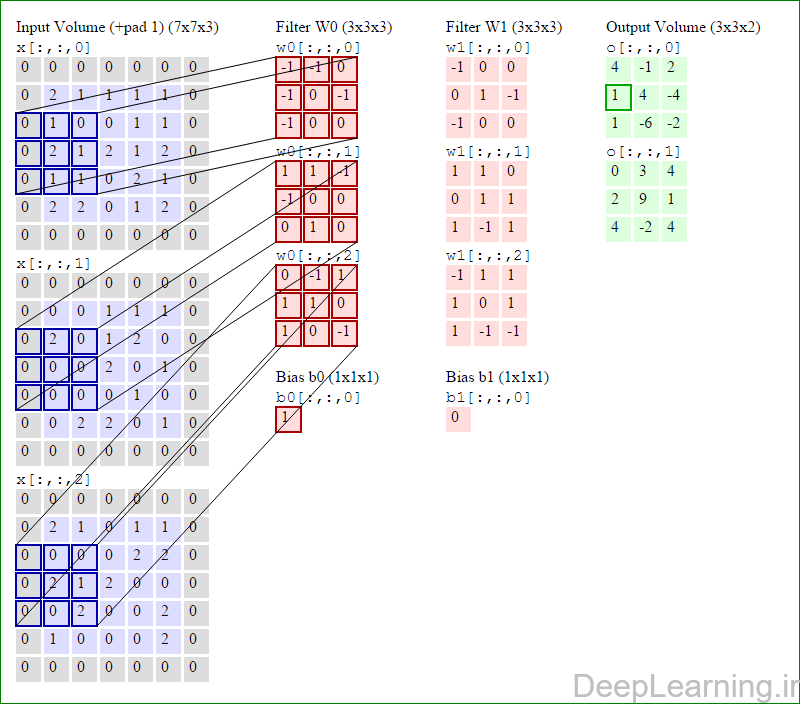
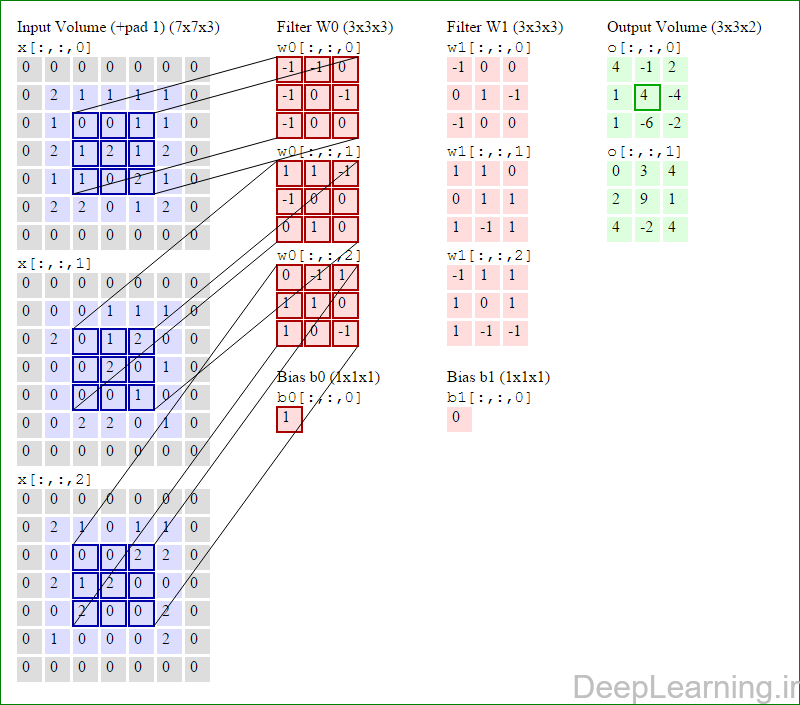
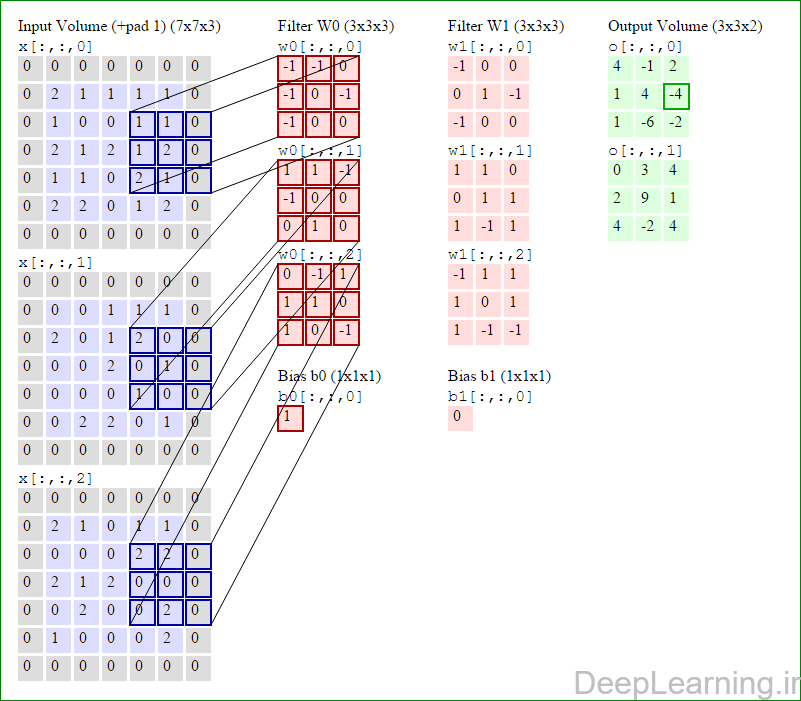
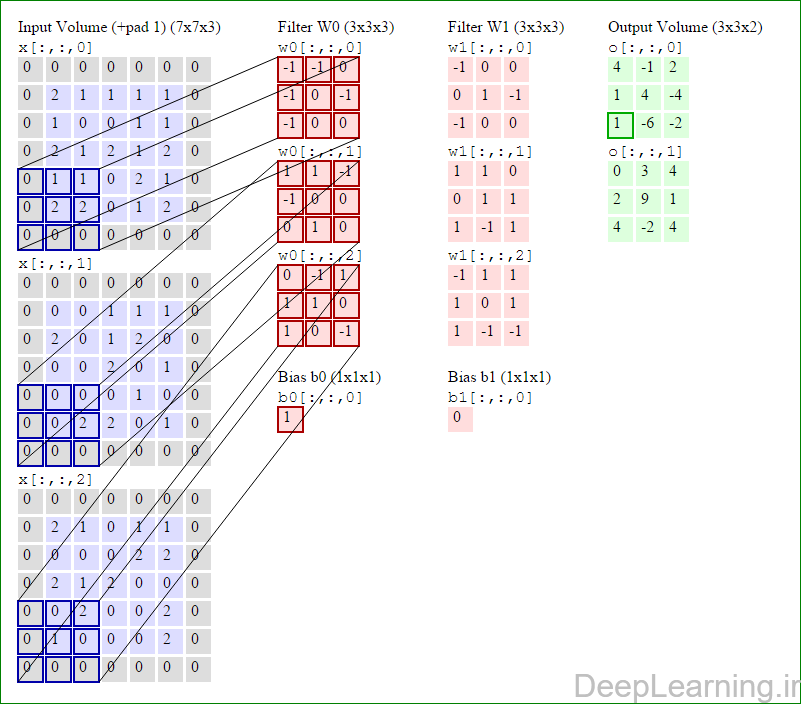
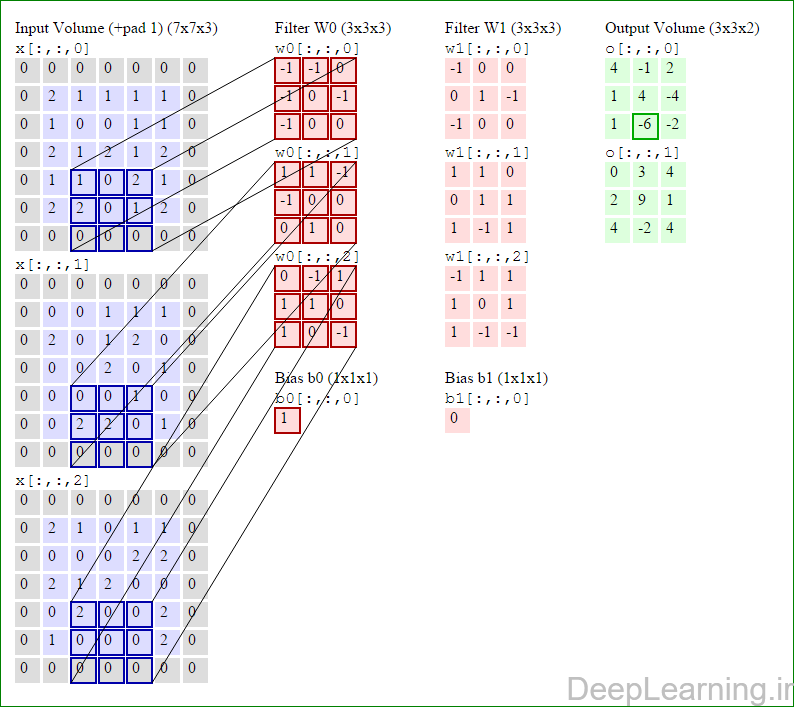
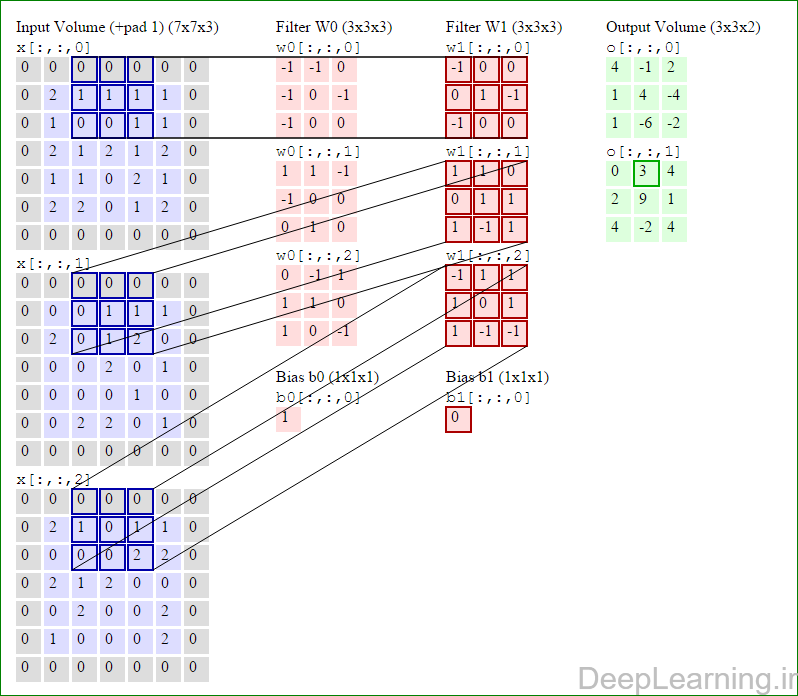
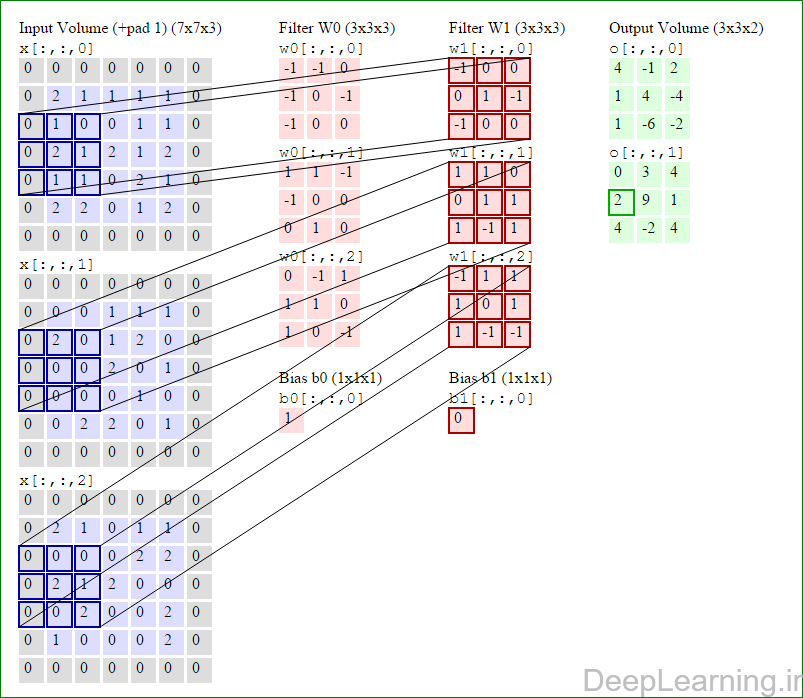
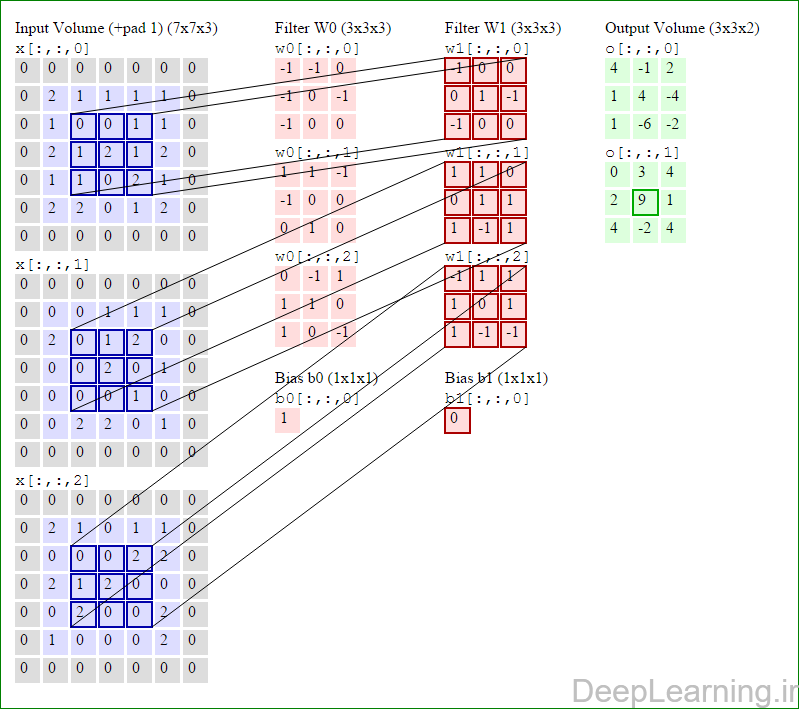
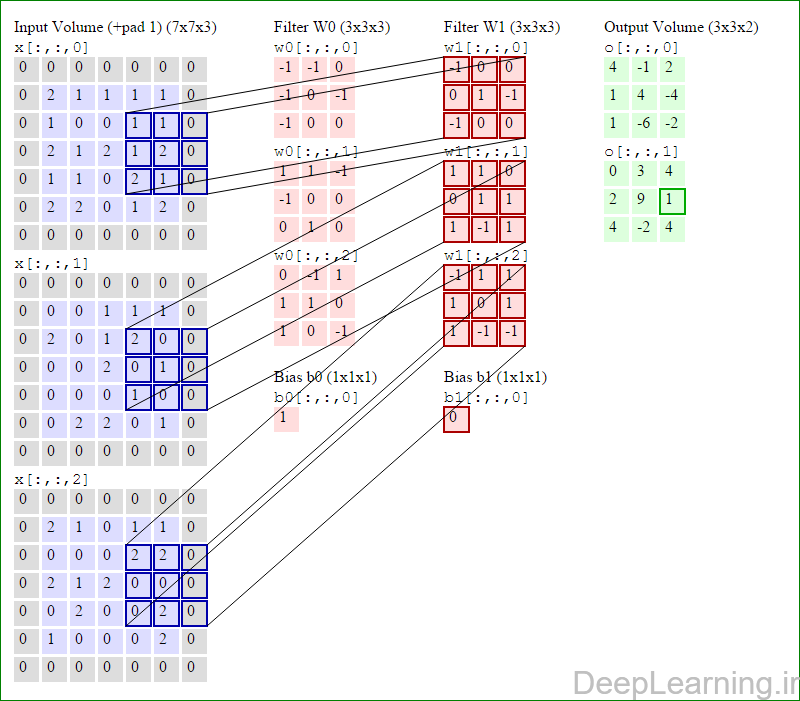
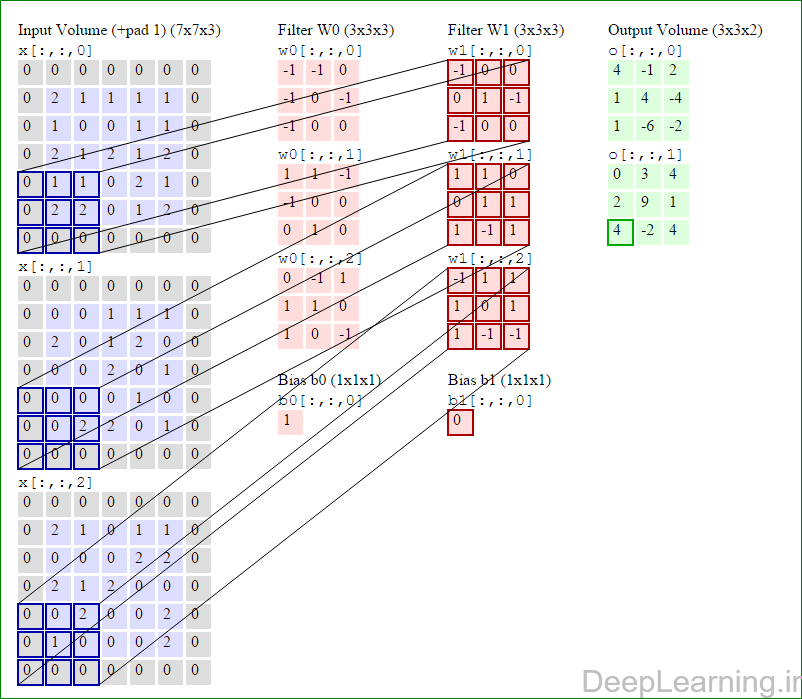
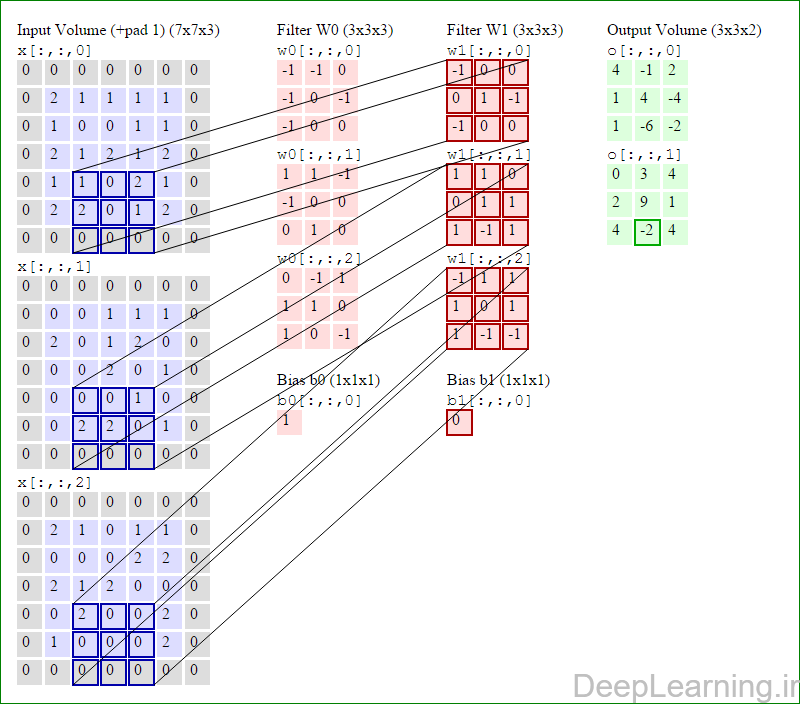
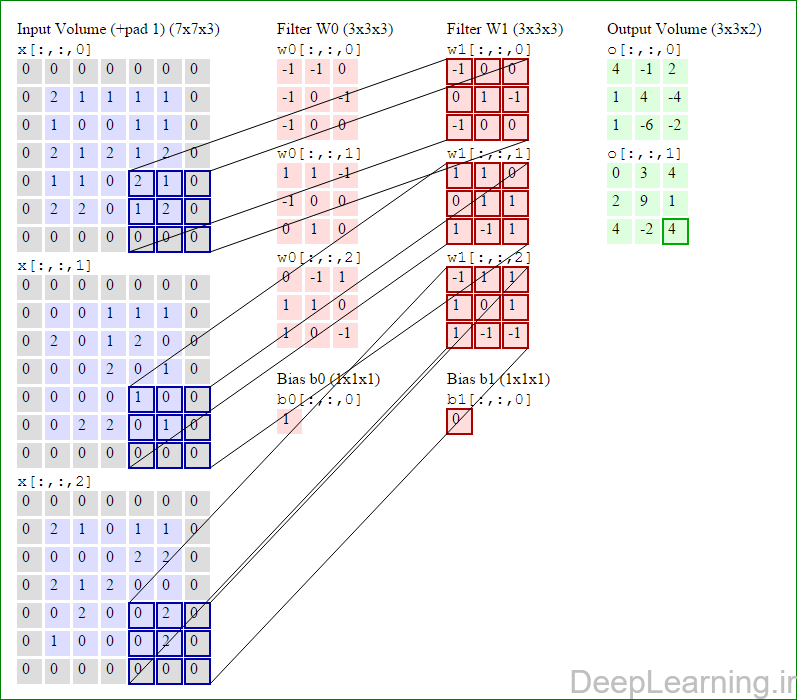
در این قسمت ما نحوه فعالیت صورت گرفته در یک لایه کانولوشن را گام بگام توسط تصویر نشان میدهیم . بخاطر اینکه نمایش حجم های سه بعدی کمی مشکل است تمام توده های سه بعدی (توده ورودی (با رنگ آبی ) , توده وزن ها ( با رنگ قرمز) و توده خروجی (با رنگ سبز) ) بصورت برش هایی نمایش داده شده اند. اندازه توده ورودی برابر با W₁ = 5, H₁ = 5,D₁= 3 میباشد( به ترتیب معرف عرض, ارتفاع و عمق) , پارامترهای لایه کانولوشن نیز به ترتیب برابر با K=2 , F = 3 , S = 2 و P =1 میباشند که به معنای آن است که ما دو فیلتر با اندازه ۳×۳ داریم که با گام (stride) S =2 بر روی توده ورودی اعمال میشوند. بنابر این اندازه توده خروجی ما هم برابر با ۳=۱+ ۲/(۲+۳-۵) خواهد بود. علاوه بر این , توجه کنید که عمل Padding با مقدار P=1 بر روی توده ورودی اعمال شده که این عمل باعث ۰ شدن مرز های بیرونی توده ورودی شده است. در تصاویر زیر میبینید که تعداد تکرار عملیات به اندازه تعداد عناصر موجود در توده خروجی( به رنگ سبز) است در تصویر مشاهده میکنید که هر عنصر در توده خروجی از ضرب عنصر به عنصر توده وزن (ماتریس وزن برنگ قرمز ) با توده ورودی (برنگ آبی) و سپس جمع تمامی عناصر با هم و نهایتا افزودن بایاس به نتیجه نهایی بدست می آید.(Convolution) بعنوان مثال برای عنصر اول توده خروجی داریم :

( (۰*-۱)+(۰*-۱)+(۰*۰)+(۰*-۱)+(۲*۰)+(۱*-۱)+(۰*-۱)+(۱*۰)+

(۰*۰))+( (۰*۱)+(۰*۱)+(۰*-۱)+(۰*-۱)+(۰*۰)+(۰*۰)+(۰*۰)+(۲*۱)+

(۰*۰))+( (۰*۰)+(۰*-۱)+(۰*۱)+(۰*۱)+(۲*۱)+(۱*۰)+(۰*۱)+(۰*۰)+

(۰*-۱) )+۱=۴

 

پایان بخش دوم آموزش

سید حسین حسن پور

بهار ۹۵

 

بعدی: آموزش شبکه کانولوشن بخش سوم

قبلی : آموزش شبکه کانولوشن بخش اول