آموزش شبکه عصبی بازگشتی بخش چهارم : معرفی GRU
بسم الله الرحمن الرحیم
در بخش قبل با چگونگی پیاده سازی یک شبکه عصبی بازگشتی معمولی آشنا شدیم. سپس در ادامه با مشکل محوشدگی گرادیان آشنا شدیم و دیدیم که این نوع شبکه ها با چه مشکلاتی مواجه اند و چگونه میتوان با این مشکلات مقابله کرد. در این بخش ما به معرفی و توضیح شبکه عصبی بازگشتی GRU میپردازیم که مشکلات شبکه عصبی بازگشتی معمولی را ندارند.
GRU – Gated Recurrent Unit
معماری GRU یا همان Gated Recurrent Unit در سال ۲۰۱۴ توسط Cho و همکاران معرفی شد.(لینک ۲) این معماری به منظور برطرف سازی کاستی های شبکه عصبی بازگشتی سنتی نظیر مشکل محو شدگی گرادیان و همچنین و همچنین کاهش سربار موجود در معماری LSTM ارائه شده است. GRU عموما به عنوان نسخه ای تغییر یافته از LSTM در نظر گرفته میشود چرا که هر دو این معماری ها از طراحی مشابه ای بهره میبرند و در بعضی از موارد بصورت یکسان نتایج عالی بدست میدهند.
GRU چگونه عمل میکند؟
همانطور که در بالا عنوان شد GRU همان نسخه بهبود یافته شبکه عصبی بازگشتی است اما چه چیزی در این معماری تغییر کرده است و چرا؟
پیشتر اشاره کردیم که برای حل مشکل محو شدگی گرادیان در شبکه عصبی سنتی یکی از راه حل ها استفاده از GRU است. این نوع معماری از مفهوم هایی بنام دروازه بروزرسانی و دروازه بازنشانی (Update gate و Reset gate) استفاده میکند. این دو اصطلاحا دروازه یا gate در اصل دو بردار اند که با استفاده از آنها تصمیم گرفته میشود چه اطلاعاتی به خروجی منتقل شده و چه اطلاعاتی منتقل نشود. نکته خاص در باره این دروازه ها این است که این دروازه ها را میتوان آموزش داد تا اینطور اطلاعات مربوط به گام های زمانی بسیار قبل را بدون آنکه در حین گذر زمان (طی گام های زمانی مختلف) دستخوش تغییر شوند حفظ کند.
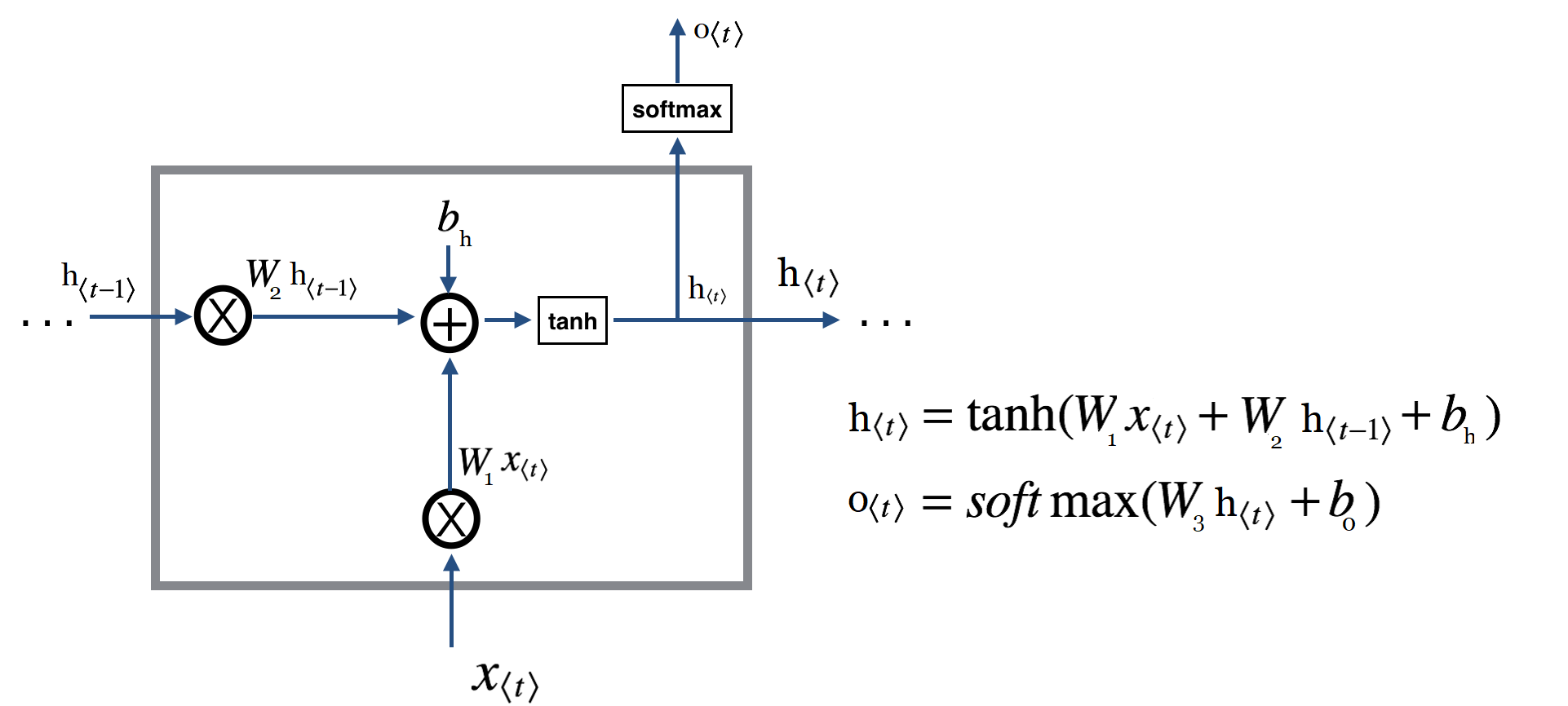
برای آنکه بهتر این موضوع را درک کنیم یکبار دیگر تصویر یک شبکه عصبی بازگشتی معمولی را ببینید :
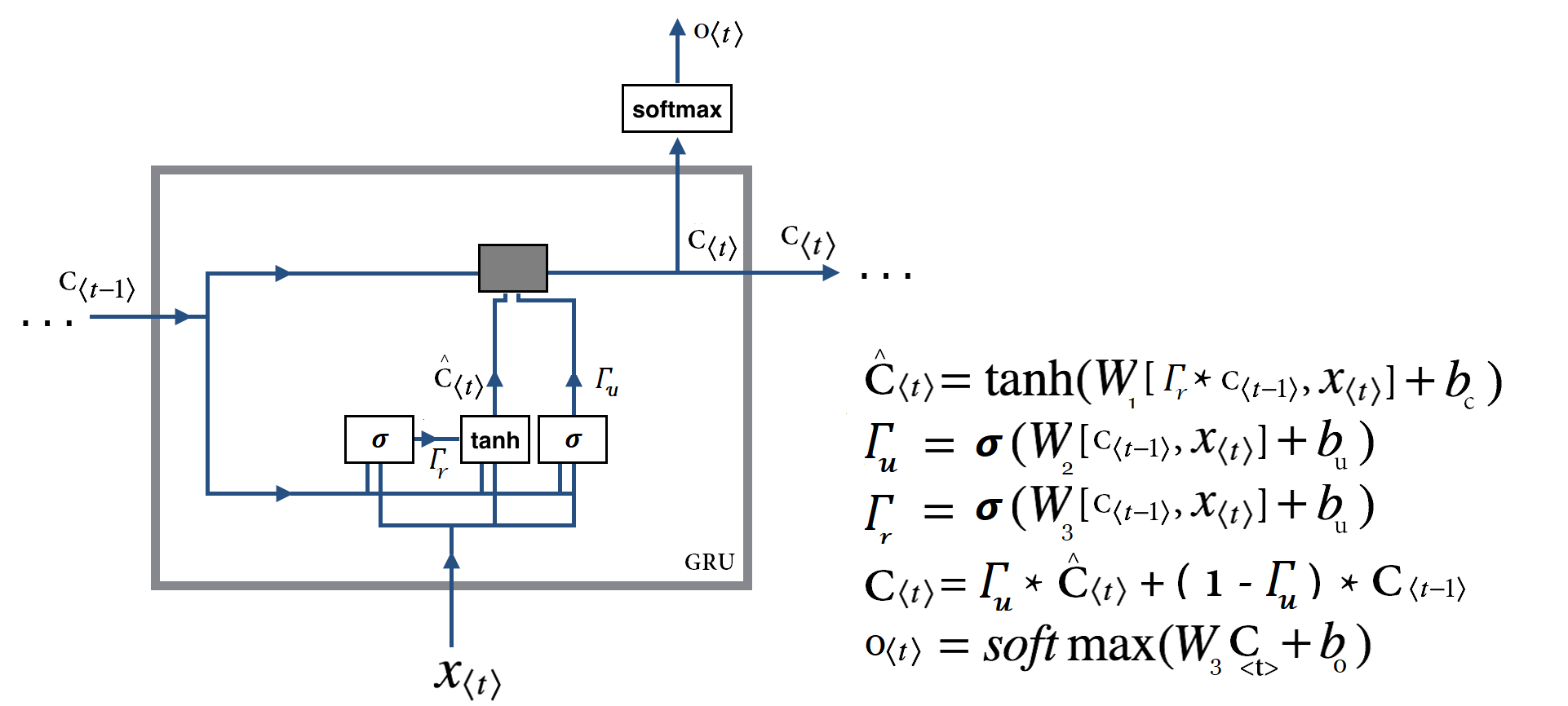
تصویری که در بالا مشاهده کردید شکل ساده شده یک سلول GRU است.(در ادامه نسخه کامل آنرا میبینیم!) اجازه دهید ببینیم در این تصویر چه چیزی در حال رخ دادن است . برای اینکار اجازه دهید روابط نوشته شده را با هم مرور کنیم :
ما قبلا گفته بودیم که یک سلول GRU بسیار شبیه یک سلول RNN سنتی است! اما روابط بالا اصلا شبیه چیزی که ما در رابطه با شبکه عصبی RNN سنتی دیدیم نیست! مشکل کجاست؟
همانطور که قبلا گفتیم واقعا عملیات صورت گرفته در GRU شبیه آنچه قبلا دیده ایم است منتها روابط اینجا کمی مختصر تر نوشته شده اند و عبارات تازه ای نیز اضافه شده است. اگر بخواهیم این روابط را باز کنیم میتوانیم آنها را بصورت زیر بنویسیم :
حالا اگر دقت کنید میبینید که در اینجا (یا همان سلول حافظه یا اصطلاحا memory Cell) در اصل همان
است که در شبکه عصبی بازگشتی RNN ما با آن آشنا شدیم و اگر خیلی راحت این عبارات را با هم جایگزین کنیم به عبارت اول در شبکه عصبی بازگشتی سنتی میرسیم. پس میبینید که عملیات اصلی یکی است اما دو عملیات دیگر نیز در اینجا داریم که در شبکه عصبی بازگشتی سنتی نداریم. قبل از اینکه به توضیح این دو عملیات جدید بپردازیم اجازه دهید ابهامات موجود را برطرف کنیم. ممکن است برای شما این سوال بوجود آمده باشد که چطور قبلا یک ماتریس وزن داشتیم (در عبارت اول) اما زمانی که این عبارات را ساده سازی کردیم تعداد ماتریس های وزن افزایش پیدا کرد در حالت اول چطور یک ماتریس وزن برای ضرب با دو بردار(
و
) که ابعاد متفاوتی دارند استفاده میشود؟ آیا نتایج این دو واقعا با هم برابر است؟
هر دو این روشها یک نتیجه را در بر دارند. در روش اول هر دو ماتریس وزن در قالب یک ماتریس وزن قرار داده شده است و به همین صورت نیز ورودی ها در قالب یک ورودی در محاسبات شرکت داده میشوند. برای انجام اینکار ما خیلی راحت آرایه ها را در راستای یک محور مشترک بهم متصل میکنیم. اجازه بدهید با هم یک مثال جزئی را ببینیم :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import numpy as np np.random.seed(1) input_dim_size = 3 hidden_state_size = 4 batch = 1 W1 = np.random.randn(input_dim_size, hidden_state_size) W2 = np.random.randn(hidden_state_size, hidden_state_size) b_h = np.random.randn(hidden_state_size) Xt = np.random.rand(batch, input_dim_size) h0 = np.zeros(shape=(batch, hidden_state_size)) result = np.tanh(np.dot(Xt, W1) + np.dot(h0, W2) + b_h) print('W1.shape : {} '.format(W1.shape)) print('W2.shape : {} '.format(W2.shape)) print('Xt.shape : {} '.format(Xt.shape)) print('h0.shape : {} '.format(h0.shape)) print('W1 : {} '.format(W1)) print('W2 : {} '.format(W2)) print('Xt : {} '.format(Xt)) print('h0 : {} '.format(h0)) # now lets stack them together W3 = np.vstack((W1, W2)) print('nNow, lets stack the weights and the inputs together: ') print('W3.shape : {}'.format(W3.shape)) print('W3 : {}'.format(W3)) Xth0 = np.hstack((Xt, h0)) print('Xth0.shape: {}'.format(Xth0.shape)) print('Xth0 : {}'.format(Xth0)) result2 = np.tanh(np.dot(Xth0, W3) + b_h) print('result.shape : {} '.format(result.shape)) print('result2.shape : {} '.format(result2.shape)) print('result : {} '.format(result)) print('result2 : {} '.format(result2)) |
و خروجی بصورت زیر خواهد بود :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
W1.shape : (3, 4) W2.shape : (4, 4) Xt.shape : (1, 3) h0.shape : (1, 4) W1 : [[ 1.62434536 -0.61175641 -0.52817175 -1.07296862] [ 0.86540763 -2.3015387 1.74481176 -0.7612069 ] [ 0.3190391 -0.24937038 1.46210794 -2.06014071]] W2 : [[-0.3224172 -0.38405435 1.13376944 -1.09989127] [-0.17242821 -0.87785842 0.04221375 0.58281521] [-1.10061918 1.14472371 0.90159072 0.50249434] [ 0.90085595 -0.68372786 -0.12289023 -0.93576943]] Xt : [[0.01936696 0.67883553 0.21162812]] h0 : [[0. 0. 0. 0.]] Now, lets stack the weights and the inputs together: W3.shape : (7, 4) W3 : [[ 1.62434536 -0.61175641 -0.52817175 -1.07296862] [ 0.86540763 -2.3015387 1.74481176 -0.7612069 ] [ 0.3190391 -0.24937038 1.46210794 -2.06014071] [-0.3224172 -0.38405435 1.13376944 -1.09989127] [-0.17242821 -0.87785842 0.04221375 0.58281521] [-1.10061918 1.14472371 0.90159072 0.50249434] [ 0.90085595 -0.68372786 -0.12289023 -0.93576943]] Xth0.shape: (1, 7) Xth0 : [[0.01936696 0.67883553 0.21162812 0. 0. 0. 0. ]] result.shape : (1, 4) result2.shape : (1, 4) result : [[ 0.39571463 -0.79928612 0.65952559 -0.87874953]] result2 : [[ 0.39571463 -0.79928612 0.65952559 -0.87874953]] |
توابع vstack و hstack که ما استفاده کردیم در اصل چیزی جز همان تابع concat در محورهای مختلف نیست. و عملا کاری که ما اینجا انجام دادیم چیزی جز متصل کردن یک ارایه به آرایه دیگر (در راستای یک محور) نیست و همینطور که در خروجی مشخص است نتایج عملیات تفکیک شده با عملیاتی که در آن وزنها و ورودی ها در یک قالب در محاسبه شرکت داده شده اند یکی است.
درمحاسبات بالا دیدیم که در یک سلول GRU ما با عملیات جدیدی مواجه هستیم که از آن با یاد میشود اما این عملیات جدید چه نقشی را ایفا میکند؟
در قسمت های قبل دیدیم که یکی از مشکلات شبکه های عصبی بازگشتی سنتی عدم توانایی آنها در بهره وری از دنباله های طولانی است. به عنوان مثال در جمله ” دانش آموزان منتخب ایران به مرحله نهایی المپیاد ریاضی رسیده و به مقام نخست دست پیدا کردند“
شبکه برای اینکه بتواند تشخیص صحیحی در انتخاب فعل انتهایی جمله داشته باشد نیازمند به خاطر سپردن “دانش آموزان” در ابتدای جمله است. و همانطور که قبلا دیدیم مکانیزم مناسبی در شبکه عصبی بازگشتی برای این مهم وجود ندارد و در بهترین حالت در یک شبکه عصبی بازگشتی سنتی چند گام محدود محلی دارای قدرت تاثیرگذاری در انتخابهای شبکه اند.(چرا که یکی از مشکلات اصلی در RNN سنتی این است که در این شبکه ها محتویات گام زمانی فعلی همیشه با یک مقدار جدید از ورودی و حالت قبلی جایگزین میشوند و اینطور اساسا قابلیت حفظ یک ویژگی از چندین گام زمانی خیلی عقب تر ممکن نیست) در شبکه عصبی بازگشتی GRU برای رفع این معضل از یک مفهوم تازه بنام دروازه بروزرسانی استفاده شده است.
بطور خیلی ساده دروازه بروزرسانی یا اصطلاحا Update Gate که با نمایش داده میشود اصطلاحا سویچی است که مشخص میکند در یک گام زمانی حالت قبلی مورد استفاده قرار گیرد یا ورودی (و یا ترکیبی از هر دو). با استفاده از این قابلیت جدید شبکه قادر است در دنباله های طولانی براحتی یک حالت از چندین گام زمانی قبل را در چند گام زمانی بعدی اثر دهد بعبارت دیگر شبکه قادر خواهد بود تا المانهایی را از گذشته دور در حافظه خود نگهداشته و از آن بهره برداری کند.
این مهم از طریق عبارت :
ایده کلی در اینجا به این صورت است که در یک گام زمانی میتوان با ۱ یا ۰ کردن گاما مشخص کرد از حالت مربوط به گام زمانی قبل استفاده شود یا حالت جدید با توجه به ورودی تازه و حالت قبلی محاسبه شود. بطور دقیقتر در اینجا شبکه میتواند با میل دادن به سمت اعداد منفی نتیجه عبارت
را به سمت صفر برده و اینطور بخش ابتدای عبارت را بی اثر و در نتیجه حالت قبلی مورد استفاده قرار گیرد و به گام زمانی بعدی منتقل میگردد. به همین صورت شبکه میتواند به حالت مابینی و حتی به عکس این مهم دست پیدا کند(با فاصله گرفتن از اعداد منفی و گرایش به سمت ۱ و بیشتر). (البته میتوان با میل وزنها به سمت صفر و بایاس به سمت منفی به همین مهم دست پیدا کرد . دقت کنید که خروجی سیگموید مد نظر ماست)
پس دروازه بروزرسانی در اینجا حکم سویچی را دارد که به شبکه این امکان را میدهد تا مشخص کند چه مقدار اطلاعات از گام های زمانی قبلی برای گام زمانی فعلی مورد نیاز است.
این قابلیت اضافه شده در GRU نسبت به همتای سنتی خود دارای ۲ فایده است:
- اول اینکه هر واحد میتواند وجود یک ویژگی خاص در جریان ورودی را برای گام های زمانی طولانی بعدی بیاد داشته باشد. هر ویژگی ای که توسط دروازه بروزرسانی GRU مهم تشخیص داده شود میتواند بدون اینکه رونویسی شده و از دست رود حفظ شود.
- نکته دوم و شاید مهمتر اینکه این قابلیت جدید در عمل مسیرهای میانبری ایجاد میکند که چندین گام زمانی را ندید گرفته و پشت سر میگذارد (از روی چندین گام زمانی میپرند) این میانبرها به همین صورت به خطای تولیدی اجازه میدهد تا بدون آنکه خیلی سریع محو شود براحتی در فاز پس انتشار منتقل گردد و اینطور معضلات مرتبط با گرادیان های محو شونده کاهش میابد.
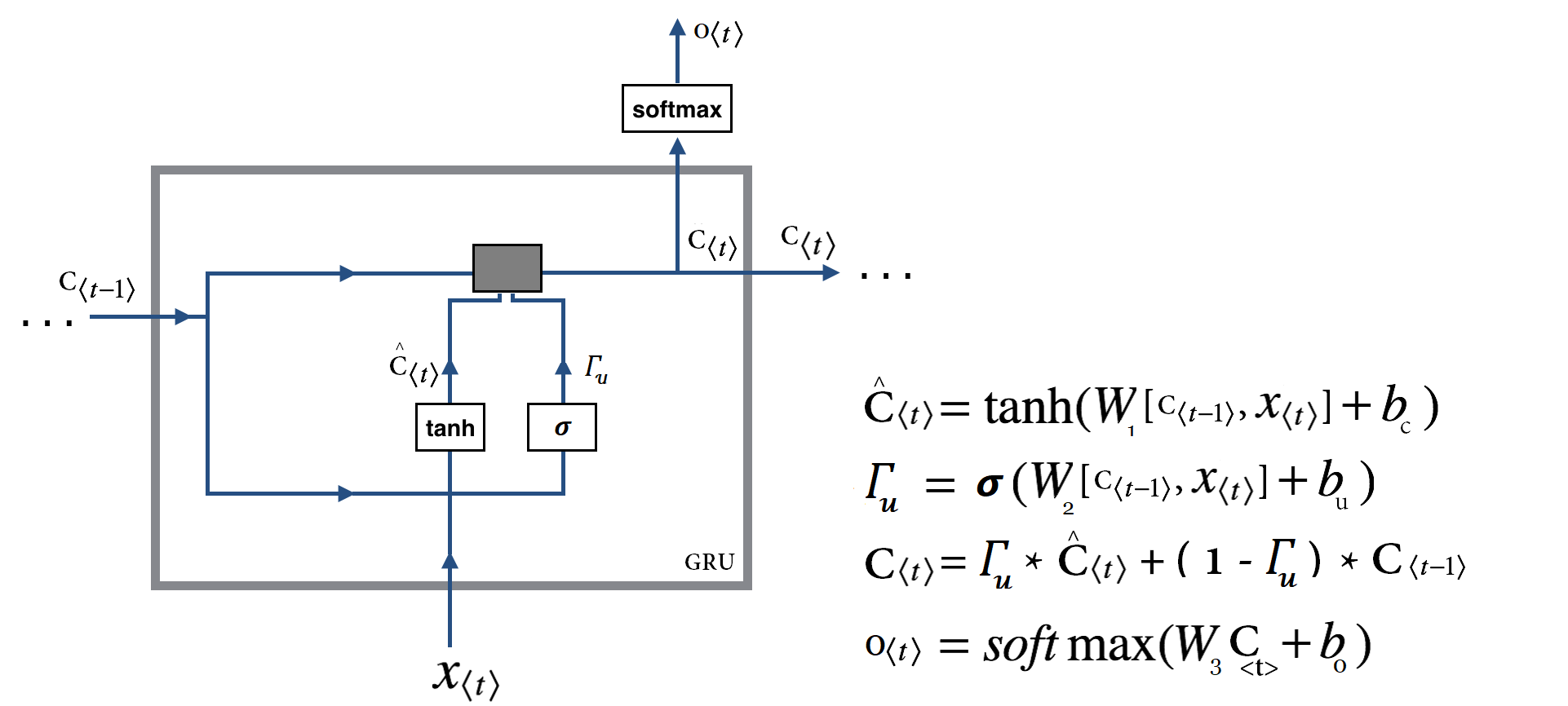
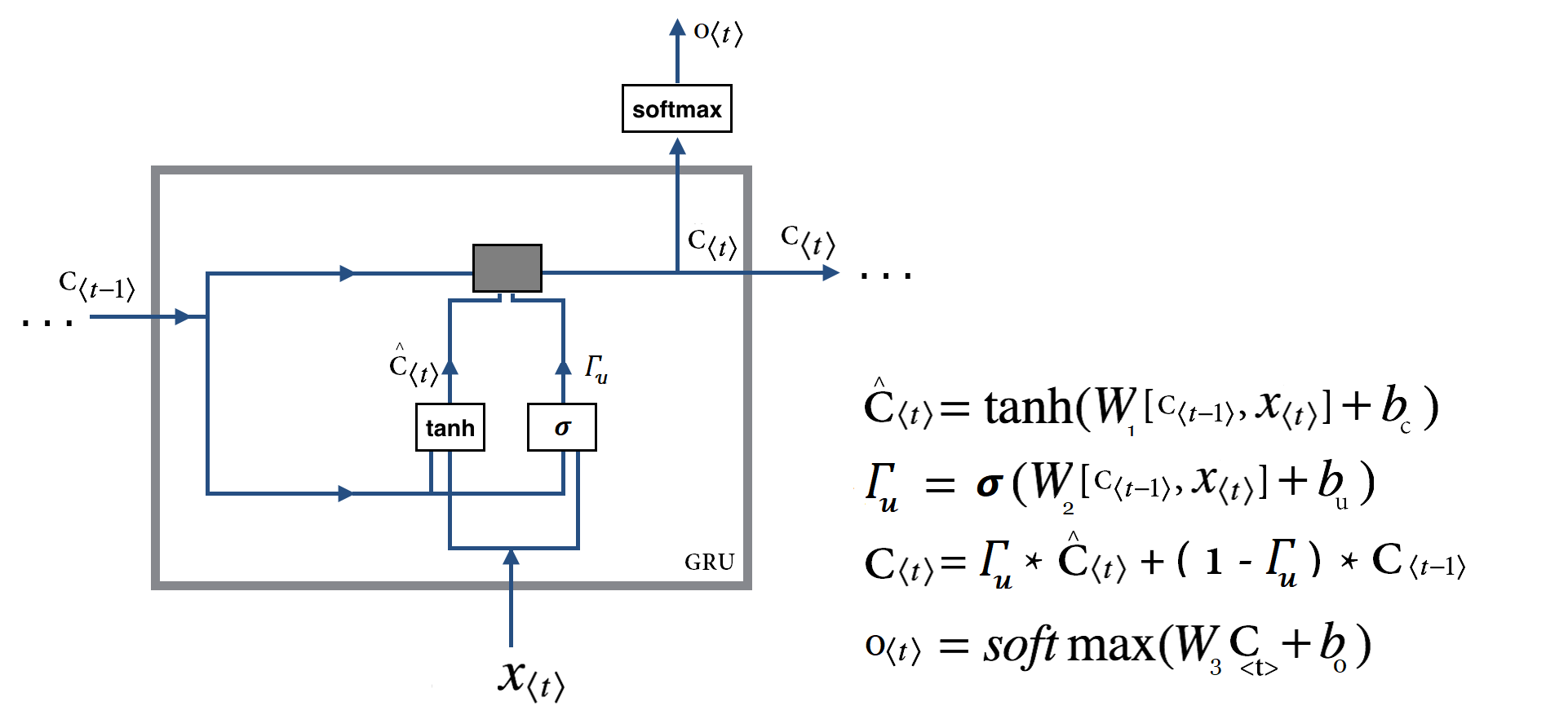
GRU کامل! :
در توضیحات اولیه که مطرح کردیم صحبت از دو دروازه کردیم اما تا به اینجا تنها در باره یک دروازه صحبت کردیم! دروازه دوم چیست و چه کاربردی دارد؟
دروازه بازنشانی یا اصطلاحا Reset Gate :
قبل از آنکه به توضیح دروازه بازنشانی بپردازیم اجازه دهید شمایل اصلی یک سلول GRU را با هم ببینیم :
همانطور که مشاهده میکنید ما با عبارات زیر مواجه هستیم و تنها تفاوت با توضیحات قبلی اضافه شدن عبارت جدیدی بنام و نقش آن در محاسبه
است :
اما این تغییرات دقیقا بدنبال رسیدن به چه چیزی هستند؟ مشکلی که در شرایط قبلی(وجود تنها یک دروازه) با آن مواجه بودیم این است که شبکه مکانیزمی جهت کنترل میزان اطلاعات منتقل شده از گام قبل را ندارد و همیشه حالت قبلی را بصورت کامل مورد استفاده قرار میدهد. این مساله با ارائه دروازه جدید که منحصرا نقش این مکانیزم را ایفا میکند مرتفع میشود. دروازه بازنشانی یا همان Reset Gate در اصل همانند سویچی عمل میکند که شبکه با کمک آن میتواند مشخص کند چه میزان از اطلاعات گذشته در گام فعلی مورد نیاز نیست (فراموش شود) و در گام فعلی از چه میزان از اطلاعات گام قبل استفاده شود. بطور دقیق تر با صفر بودن این سویچ این دروازه در عمل شبکه را وادار میکند بگونه ای عمل کند که گویا در حال خواندن اولین بخش از دنباله ورودی است و اینطور شبکه را قادر به فراموشی حالت محاسبه شده قبلی میکند و به همین صورت میتواند با فاصله گرفتن از صفر حالت مابینی را فراهم آورد.
با کمک این دو قابلیت جدید شبکه عصبی GRU براحتی میتواند نسبت به ذخیره سازی و یا فیلتر کردن اطلاعات از گام های زمانی قبلی اقدام کرده و از دنباله های طولانی که شبکه عصبی بازگشتی سنتی در مواجه با آن با مشکلات عدیده ای مواجه بود بهره برداری کند و کاستی های شبکه عصبی بازگشتی سنتی را مرتفع سازد. این نوع شبکه ها بسیار قدرتمند بوده و بواسطه سربار کمتر آنها نسبت به LSTM و قدرت بیشتر آنها نسبت به RNN های سنتی مورد استفاده گسترده قرار گرفته اند.
در بخش بعدی انشاءالله به معرفی شبکه عصبی LSTM میپردازیم و با قابلیت ها و ویژگی های این شبکه آشنا خواهیم شد.




[…] آموزش شبکه عصبی بازگشتی بخش چهارم : معرفی GRU […]
عذر میخوام من این مقاله رو خوندم، مقاله ی مرجع ای که رفرنس داده بودید رو هم خوندم و یک سری مقالات دیگه که از این روش استفاده کردن هم نگاه کردم. ولی مطلبی که برام سواله و جا نیوفتاد اینه که ساختار کلی شبکه عصبی ای که بخوایم GRU باشه چجوریه ؟ چند لایه داره چند نرون داره؟ چون مثلا تو هر شبکه عصبی یا شبکه عمیق مشخصه که یه تعداد لایه داریم و هر لایه چه خصوصیتی داره ولی برای شبکه GRU یک ساختار کلی معرفی شده و در مابقی سایت ها و ویدیو ها هم همینطوره
ولی سوال من اینه که الان من بخوام یه شبکه عصبی از نوع GRU داشته باشم که یه سری داده سری زمانی بهش بدم، باید مثل شبکه عصبی معمولی چند لایه در نظر بگیرم؟ اگر بله اونوقت هر لایه یا هر نرون میشه یه دونه از اینا (GRU) یعنی هر نرون یه GRU عه یا هر لایه یه GRU عه ؟؟
اگرم خیر، یعنی مثل شبکه عصبی معمولی نباید در نظر بگیریم پس کلا چجوری میشه شبکه ما؟
خیلی روی این موضوع گیر کردم ممنون میشم منو از این ابهام نجات بدید.
با تشکر
سلام.
یک واحد GRU هست که شمایلش و شیوه کار باهاش توضیح داده شده. هر واحد هم یک لایه GRU در نظر گرفته میشه.
نمونه های چند لایه هم هستن که از ترکیب چند GRU روی هم تشکیل شدن(مثلا خروجی hidden state ها از GRU قبلی به بعدی منتقل میشه و از خروجی مثلا GRUدوم استفاده میشه)
اندازه hidden state یی که برای هر واحد بازگشتی مشخص میکنید حکم تعداد نورون پردازشی رو در این نوع شبکه ها داره.
از نظر داخلی بخوایید ببینید تعداد گام های زمانی که دارید معرف تعداد لایه های درونی هر واحد بحساب میاد.
از بیرون اگر نگاه کنید در کنار ترکیب با لایه های دیگه مثلا معمولا نرمش اینه از یک یا دو واحد(لایه) بازگشتی استفاده میشه.(البته بسته به ماهیت کار هم داره)
یه فریم ورک انتخاب کنید باهاش سعی کنید مساله ای رو حل کنید براحتی میاد دستتون پارامترهای تاثیر گذار چی هستند و چطور باید پیش برید.
بی نهایت سپاسگزارم از توضیحتون
تا حدی دستم اومد که قضیه چجوریه
فقط یه نمونه فریم ورک که میشناسید معرفی میکنید برم سرچ کنم ببینم چیه و … ؟
با تشکر
سلام
Pytorch, Tensorflow/Keras دوتا نمونه هستن که میتونید چک کنید
آهان بله تا حدودی آشنایی دارم با Tensorflow و Keras
ممنون
یه سوال دیگه، اینکه گفتید (( از نظر داخلی، تعداد گام های زمانی که دارید معرف تعداد لایه های درونی هر واحد بحساب میاد.)) منظورتون از تعداد لایه های درونی هر واحد، تعداد گیت های update یا reset عه، یا منظورتون اینه که به تعداد گام های زمانی، در ساختار شبکه، به همون تعداد GRU داریم؟
دررابطه با این هم اگه میشه یه خرده بیشتر توضیح بدید ممنون میشم (( از بیرون اگر نگاه کنید در کنار ترکیب با لایه های دیگه مثلا معمولا نرمش اینه از یک یا دو واحد(لایه) بازگشتی استفاده میشه.(البته بسته به ماهیت کار هم داره))
مثلا اگر بخوایم تو یه شبکه عصبی یک یا دو لایشو از GRU استفاده کنیم، مابقی لایه ها عموما از چه نوعی انتخاب میشه؟ LSTM؟ RNN؟ یا یه شبکه عصبی معمولی؟!
سلام.
چیزی که گفتم بیشتر در جهت ایجاد درک از شیوه کار این شبکه ها با توجه به شبکه های معمولی بوده. (مباحث مربتط با vanishing gradient و… که در یک واحد GRU میبینید یا شیوه کار این واحد با این تصویر سازی بهتر متوجه میشید)
اگر آموزش اول رو ببینید و همینطور این بخش این شیوه در کدها و توضیحاتی که نوشتم و توضیح دادم کاملا مشخصه .
LSTM و GRU و RNN انواع مختلفی از لایه های بازگشتی هستن معمولا یکی از اینها رو در شبکه اتون استفاده میکنید یا GRU یا LSTM. عموما LSTM استفاده بیشتری داره اما سربار GRU کمتره و در برخی کاربردها اون استفاده بیشتر میشه.
شبکه عصبی معمولی یا غیر معمولی نداریم. دقت کنید ما لایه های مختلف داریم اگه بگید شبکه عصبی معمولی یعنی MLP? یا چیز دیگه؟ تعریف این شبکه مشخصه همه لایه ها به چه صورتیه
شبکه عصبی کانولوشن مشخصه تعریفش یعنی از لایه های کانولوشنی بهره میبره
شبکه عصبی LSTM به این اشاره میکنه که شبکه ای هست که درش از LSTM استفاده شده صرفا یا بخش قابل توجهی از اون.
شبکه های ترکیبی هم هست که از ترکیب لایه های مختلف و …. ایجاد میشه. این دیگه بسته به کاربرد مورد نظر شما داره که نیاز به چه عملیاتی داشته باشید در یک مدل و برای اون عملیات از چه چیزی استفاده کنید.
آهان بله بسیار عالی، الان کامل متوجه شدم.
البته مواردی که فرمودید هم مطالعه کرده بودم، اما مجدد مقاله ی مرجع GRU رو که مطالعه کردم دیدم گفته که ۳ مدل RNN در نظر گرفته که یکی RNN-GRU یکی RNN-LSTM و دیگری RNN معمولی بوده و نتایج اینارو با هم مقایسه کرده. اینجا متوجه شدم که مثلا میشه شبکه RNN باشه و یکی ۲ تا لایه هم GRU داشته باشه. مشابه پاسخ قبلی شما.
قبلش فکر میکردم کل یه شبکه از لایه اول تا آخر رو مثلا GRU میذارن.
منظورم از شبکه عصبی معمولی هم همون MLP بود 😉
ولی در نهایت درست می فرمایید باید ببینم کدوم حالت و چه نوع شبکه ای مورد نیاز من خواهد بود.
بی نهایت از وقتی که گذاشتید و با حوصله پاسخ دادید ممنونم.
با سلام و ممنون از مطالب مفیدتون.
می خواستم بدونم مثلا میشه یه شبکه Rnn رو با نمونه برداری از”y=2x^2+4x+2″ آموزش داد بعد به شبکه آموزش داده شده نمونه های “y=3x^2+x+1” رو داد؟
منظورم اینکه با یک وروردی آموزش ببینه و برای تخمین سری زمانی از همون جنس ولی با ضرایب متفاوت بکار بره.
سلام
شاید بیان مساله به این شکل صحیح نباشه. شبکه های عصبی universal (function) approximator هستند و و هر تابعی رو میتونن تخمین بزنن (با فرض وجود ظرفیت و داده و شرایط آموزشی مناسب)
شبکه سعی میکنه تابعی که داده های شما از اون مشتق شده رو تخمین بزنه و در همون حوزه هم بدرستی عمل میکنه. برای اینکه بهتر متوجه بشید صورت ساده شده مساله رو در نظر بگیرید
در نظر بگیرید x شما حاوی مقادیر ورودی مختلف میتونه باشه (نقش ورودی) پس شبکه برای تخمین درست تابع شما باید دوتا پارامتر تتا رو بدست بیاره که اینجا ضرایب شما خواهند بود. (بایاس هم قائدتا باید محاسبه بشه ولی تمرکز روی پارامترها هست اینجا)
تتا همون پارامتر یا وزنهای شما هست. وقتی شبکه روی یک تابع آموزش ببینه روی همون موارد معتبر هست.
اگر قراره شبکه روی چیزی بدرستی جواب بده لازمه اش اموزش دیدن روی داده هایی از همون جنسه.
این مقاله شاید براتون جذاب باشه خوندنش
ممنون از جوابتون. یک سوال دیگه هم داشتم ممنون می شم جواب بدین. از سوال قبلی بیشتر مقصودم این بود که مثلا شبکه از ورودی های تابع اول بتونه یاد بگیره که سری زمانی که دریافت می کنه نوعش درجه دو هست. بعدش با توجه به وزن هایی که گرفته، بتونه با سه چهارتا نمونه از تابع دوم سریع به تابع دوم فیت بشه و نیاز به یک آموزش کامل نداشته باشه. چون بالاخره هر دو تابع درجه دو هستن. البته با توجه به توضیحات شما احساس کردم Rnn این قابلیت رو نداره محض اطمینان دوباره پرسیدم.
یا مثال دیگه مثلا شبکه هایی که قیمت یک سهم رو پیش بینی می کنن دو تا مساله پیش میاد یکی اینکه آیا میشه از یک شبکه آموزش دیده شده روی یک سهم برای سهام دیگه هم استفاده کرد که طبق فرمایش شما گویا نمیشه. مسئله دوم حتی اگه یک شبکه برای یک سهم آموزش ببینه وقتی بازار بسته میشه و فردا دوباره شروع میشه آیا این قطع شدن و تغییر ساعت رو تاثیر می دن یا همون مقدار آخر رو مقدار اولیه فردا در نظر می گیرن؟
بابت مقاله خوبی که معرفی کردین ممنون. ببخشید اگه سوال طولانی شد
سلام
اینکه شما دنبال این باشید که شبکه تشخیص بده تابعی درجه اش چنده یه بحثه و با اینکه شبکه رو یه تابع درجه دو آموزش ببینه و بعد بتونه رو تمام توابع(یا هر تابع درجه دو دیگه ای) درجه دو دیگه بدرستی کار کنه یه بحث دیگه اس (این عملی نیست بصورت پیشفرض و بسادگی) برای همین اون لینک رو دادم که مطالعه کنید تا اگر بحثتون مشابه هست بهتون کمک کنه.
متاسفانه من تو پیش بینی سهام فعالیتی نداشتم و نمیتونم کمکی کنم. این حوزه برخلاف برداشت اولیه از اون، خیلی پیچیده اس و قلق ها و نکات زیادی داره برای اینکه بشه یک مدلی رو ترتیب داد که بصورت مناسبی کارش رو انجام بده. این سوال رو باید از عزیزانی بپرسید که بصورت تخصصی کار کردن و تجربه خوبی دارن تو این حوزه تا بتونن راهنماییتون کنن.
با سلام و تشکر از این پست بسیار خوبتون. یک سوال داشتم در مورد اواسط متن که گفتین:
“در اینجا شبکه میتواند با میل دادن W_2 به سمت صفر نتیجه عبارت Gamma_u را به سمت صفر برده و اینطور بخش ابتدای عبارت را بی اثر و در نتیجه حالت قبلی مورد استفاده قرار گیرد و به گام زمانی بعدی منتقل میگردد. ” ولی خب مگه گاما از تابع سیگموید بدست نمیاد؟ پس وقتی وزن ۲ به صفر میل بکنه اون هم به نیم میل میکنه. در نتیجه باید گفت شبکه با میل دادن وزن ۲ به مقادیر منفی میتواند گاما را صفر و بخش ابتدایی بی اثر می شود.
سلام
بله فرمایش شما درسته .
من خروجی سیگموید رو در نظر نگرفته بودم.
البته از این جهت هم میتونید ببینید که با میل وزن w2 به سمت صفر و میل بایاس به سمت یک عدد منفی باز نتیجه همون میشه.
اما در هر صورت نظر شما کاملا صحیح بود و مثالی که من زدم دقیق نبود و الان تصحیح شد و خیلی ممنونم بابت اشاره شما به این مطلب.
انشاءالله در پناه خداوند همیشه موفق و سربلند باشید
سلام
با تشکر از زحمات شما.
من یک کد پیدا سازی GRU رو از سایتی که در اختیار گذاشته بود داخل جوپیتر اجرا کردم و مشکلی نداشت، حالا یک سری تغییرات خیلی کمی لازم هست که اعمال کردم، همه چیز به نظر درست میاد ولی خطا میده و نمی دونم که به چه خاطر هست؟ از تیانو استفاده شده.
ValueError Traceback (most recent call last)
in
۳۲
۳۳ # Build model
—> 34 model = GRUTheano(VOCABULARY_SIZE, hidden_dim=HIDDEN_DIM, bptt_truncate=-1)
۳۵
۳۶ # Print SGD step time
~\gru-test-01\gru_theano.py in __init__(self, word_dim, hidden_dim, bptt_truncate)
۳۹ # We store the Theano graph here
۴۰ self.theano = {}
—> 41 self.__theano_build__()
۴۲
۴۳ def __theano_build__(self):
~\gru-test-01\gru_theano.py in __theano_build__(self)
۹۵ dict(initial=T.zeros(self.hidden_dim)),
۹۶ dict(initial=T.zeros(self.hidden_dim)),
—> 97 dict(initial=T.zeros(self.hidden_dim))])
۹۸
۹۹ prediction = T.argmax(o, axis=1)
~\Anaconda3\lib\site-packages\theano\scan_module\scan.py in scan(fn, sequences, outputs_info, non_sequences, n_steps, truncate_gradient, go_backwards, mode, name, profile, allow_gc, strict, return_list)
۷۷۲ # and outputs that needs to be separated
۷۷۳
–> 774 condition, outputs, updates = scan_utils.get_updates_and_outputs(fn(*args))
۷۷۵ if condition is not None:
۷۷۶ as_while = True
~\Anaconda3\lib\site-packages\theano\scan_module\scan_utils.py in get_updates_and_outputs(ls)
۵۷۳ raise ValueError(error_msg)
۵۷۴ else:
–> 575 raise ValueError(error_msg)
۵۷۶
۵۷۷
ValueError: Scan cannot parse the return value of your lambda expression, which is: [Subtensor{int64}.0, Elemwise{add,no_inplace}.0, Elemwise{tanh,no_inplace}.0, [Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0, Elemwise{add,no_inplace}.0]]