آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش دوم : Forward

توسط سید حسین حسن پور متی کلایی در مارس 24, 2019 آخرین بروزرسانی جولای 2, 2019

بسم الله الرحمن الرحیم

در بخش قبل مباحث تئوری و کلی در رابطه با شبکه های عصبی بازگشتی مطرح شد. در این بخش ما وارد جزییات بیشتری شده و سعی میکنیم بصورت عملی در مورد چیستی و کارکرد این گونه شبکه ها صحبت کنیم . با هم نسبت به پیاده سازی این شبکه در زبان پایتون اقدام کنیم و بعد یک نمونه مثال را از نظر بگذرانیم تا در نهایت به درک مناسبی در این زمینه دست پیدا کنیم .

RNN‌ها یا شبکه های عصبی بازگشتی چیستند؟‌

همانطور که در بخش اول عنوان شد ایده پشت شبکه های عصبی بازگشتی یا اصطلاحا RNN ها استفاده از اطلاعات سِری یا دنباله ای (اصطلاحا Sequential) است. در یک شبکه عصبی سنتی فرض ما بر این است که تمام ورودی ها نسبت به یکدیگر مستقل هستند اما برای بسیاری از کاربردها و وظایف این فرض ساده ما صادق نیست. به عبارت دقیق تر اگر بخواهیم کلمه بعدی در یک جمله را پیش بینی کنیم لازم است بدانیم کلمات قبل از آن چه کلماتی بوده اند. به همین دلیل RNN‌ها به بازگشتی معروف شده اند چرا که یک عملیات یکسان را بر روی تمامی المان های یک دنباله (یا سری) از ورودی ها اعمال میکنند و در این حالت خروجی تولید شده وابسته به محاسبات قبلی خواهد بود.

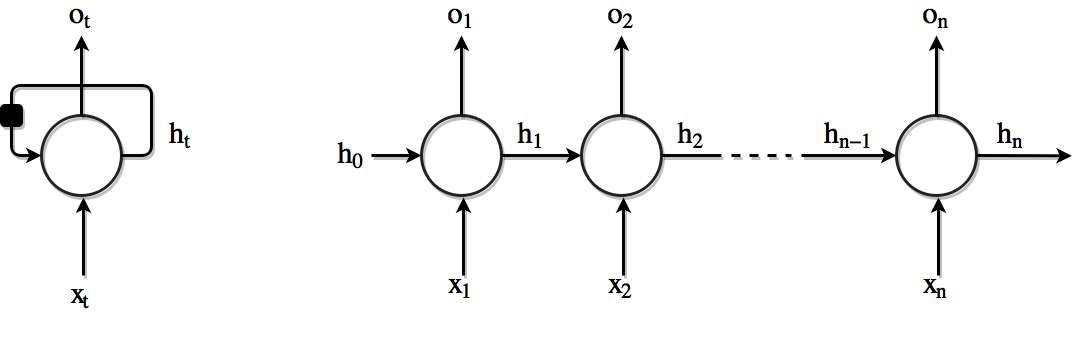
از زاویه دیگری نیز میتوان به این قضیه نگاه کرد به این شکل که RNN ها را گونه ای شبکه های عصبی در نظر گرفت که دارای یک حافظه داخلی هستند که اطلاعاتی را در مورد آنچه که تا بحال محاسبه شده است در خود نگه میدارند. در تئوری شبکه های RNN (معمولی) میتوانند از اطلاعات در دنباله های بسیار طولانی استفاده کنند اما در عمل این نوع شبکه ها واقعا محدود به چند گام قبل تر هستند و قادر به پشتیبانی از دنباله های بسیار طولانی نیستند. در زیر تصویری از یک RNN معمولی را مشاهده میکنید :‌

همانطور که در بخش قبل دیدیم شکل بالا چگونگی باز شدن (یا اصطلاحا unroll یا unfold شدن) یک لایه RNN را نشان میدهد. بازسازی یا اصطلاحا unfolding/unrolling به این معناست که ما یک لایه RNN را برای کل دنباله ورودی نمایش میدهیم. بعنوان مثال اگر دنباله ما جمله ای با ۵ کلمه باشد شبکه ما بصورت یک شبکه عصبی ۵ لایه در خواهد آمد که هر لایه به یک لغت ورودی اختصاص داده خواهد شد. هر لایه RNN حاوی محاسباتی است که در زیر مشاهده میکنید :

محاسبات دخیل در یک RNN بصورت زیر هستند :‌

‌ $x_{t}$ ورودی در گام زمانی $t$ است. بعنوان مثال $x_{1}$ میتواند یک بردار one hot شده متناظر با دومین کلمه یک جمله باشد.
$h_{t}$ (که با $s_{t}$ هم شناخته میشود) یک حالت مخفی در گام زمانی $t$ است. این همان حافظه شبکه است. $h_{t}$ بر مبنای حالت قبلی و ورودی در گام فعلی محاسبه میشود :‌ $h_t = f(W_1 \cdot X_t +W_2 \cdot h_{t-1})$ .
تابع $f$ معمولا یک تابع غیرخطی مثل tanh‌ و یا relu است. $t-1$ که برای محاسبه اولین حالت مخفی مورد نیاز است معمولا با صفر مقداردهی اولیه میشود.
‌ $o_{t}$ خروجی در گام $t$ ‌ است. بعنوان مثال اگر ما بخواهیم کلمه بعدی در یک جمله را پیش بینی کنیم این برابر با برداری از احتمالات برگرفته از لغت نامه ما خواهد بود. $o_t = softmax(W_3 \cdot h_t)$

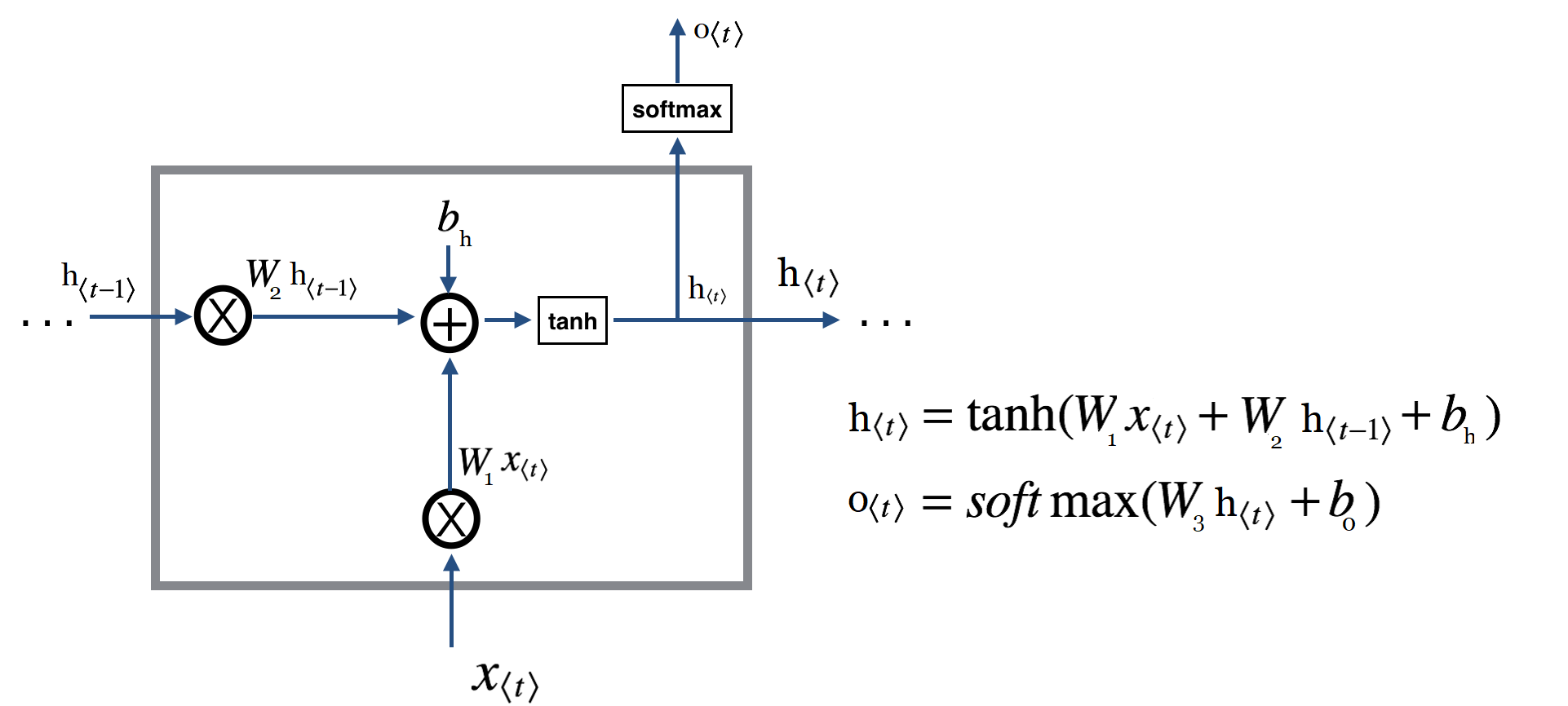
پس بصورت خلاصه رابطه های مورد نیاز بصورت زیر هستند:

$h_t = tanh(W_1 \cdot X_t +W_2 \cdot h_{t-1} )$

$o_t = softmax(W_3 \cdot h_t )$

در اینجا بجای تابع کلی f از tanh استفاده کردیم.

دقت کنید ما میتوانیم مثل یک شبکه عصبی سنتی یک عبارت بایاس هم به عبارت فوق اضافه کنیم :

$h_t = tanh(W_1 \cdot X_t +W_2 \cdot h_{t-1} + b_h)$

$o_t = softmax(W_3 \cdot h_t + b_o)$

این عبارات شاکله اصلی یک لایه RNN را تشکیل میدهند.

نکته :‌
همانطور که پیشتر اشاره کردیم ما میتوانیم حالت مخفی $h_{t}$ را بعنوان حافظه شبکه نیز در نظر بگیریم . $h_{t}$ اطلاعاتی درباره آنچه در گام های زمانی قبلی رخ داده است را در خود نگهداری میکند. خروجی در گام $o_{t}$ صرفا بر اساس حافظه در زمان $t$ ‌ محاسبه میشود. همانطور که بصورت خلاصه در بالا عنوان شد در عمل این مکانیزم حافظه در شبکه های RNN معمولی قادر به بهره برداری از گامهای طولانی نیست یعنی $h_{t}$ معمولا قادر نیست اطلاعات را از تعداد زیادی گام زمانی قبلتر حفظ کند و در نتیجه محدود به چند گام زمانی اخیر است. برای رفع این مشکل ما از انواع دیگر این نوع از شبکه استفاده خواهیم کرد. اما قبل از آن به بیان کامل شبکه RNN معمولی می پردازیم چرا که مفاهیم اصلی و پایه یکسانی دارند و با درک این مبانی به آسانی میتوان شیوه کارکرد و نقاط مثبت روشهای بهبود یافته بعدی را بخوبی دریافت.

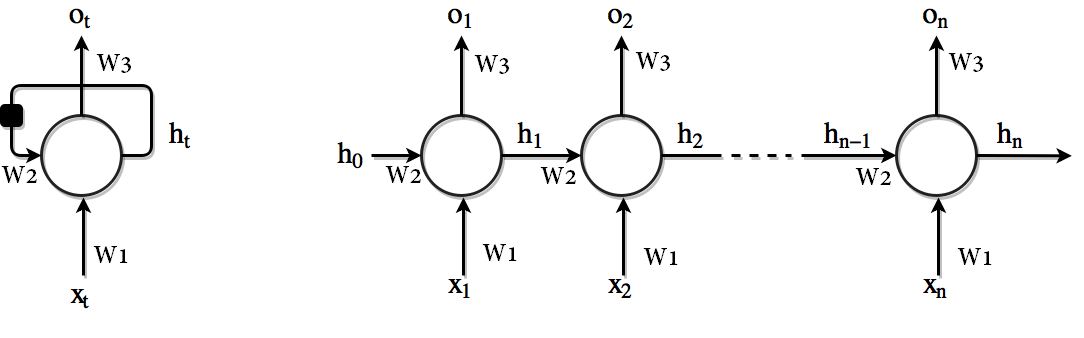
برخلاف شبکه عصبی عمیق سنتی که از پارامترهای مختلف در هر لایه بهره میبرند در یک شبکه RNN از پارامترهای یکسان در تمامی گامها بهره برده میشود. ( $W_3$ $W_2$ $W_1$ در فرمول های بالا). یعنی هر لایه RNN تنها دارای تعداد معینی پارامتر است که در تمامی گام های زمانی از آنها بصورت اشتراکی استفاده میشود. unrolling یک لایه RNN که در تصویر بالا مشاهده میکنید این مساله را بخوبی نشان میدهد. این مساله نمایانگر این حقیقت است که ما در هر گام تنها ورودی متفاوت داشته و عملیات یکسان برروی ورودی های متفاوت صورت میگیرد. در نتیجه این مساله باعث کاهش قابل ملاحظه تعداد پارامترهایی مورد نیاز جهت یادگیری میشود.
شکل بالا دارای خروجی در هر گام است اما الزاما همیشه اینگونه نیست و این مساله وابسته به کاربرد مورد نظر ما میباشد. بعنوان مثال زمانی که قصد تحلیل احساسات بر روی یک جمله را داشته باشیم ما تنها به خروجی نهایی نیاز داریم و نیازی به دریافت خروجی بعد از هر لغت نداریم. به همین صورت ممکن است ما نیازی به ورودی در همه گام های زمانی نداشته باشیم. ویژگی اصلی یک RNN حالت مخفی آن است که بعضی از اطلاعات مرتبط با یک دنباله را در خود نگهداری میکند.

h برداری است که اندازه آنرا ما مشخص میکنیم . خروجی نیز همانطور که قبلا اشاره شد وابسته به کاربرد است . عموما چند نوع ورودی و خروجی میتوانیم داشته باشیم که پیشتر در بخش اول به آن اشاره کردیم .

پیاده سازی :

خب اکنون اجازه دهید با هم سعی کنیم و یک لایه RNN را پیاده سازی کنیم . این لایه RNN ساده دارای یک فاز forward و یک فاز backward میباشد و سعی میکنیم که بصورت گام بگام هر دو بخش را پیاده کنیم. بعد از انجام این کار بایستی به درک مناسبی از شیوه کار این نوع شبکه عصبی رسیده باشید. اگر بعد از این بخش کماکان موارد مبهمی برای شما وجود داشته باشد در بخش بعدی که نوبت به حل یک مساله ساده است انشاءالله این موارد نیز مرتفع خواهند شد.

قبل از شروع به پیاده سازی لازم است مواردی را بعنوان نماد مشخص کنیم .

تا به اینجا یادگرفتیم که یک شبکه عصبی RNN بطور خلاصه بصورت زیر است :

و اگر گام زمانی ما برابر ۱ باشد میبینیم که تنها نیاز به پیاده سازی دو عملیات بسیار ساده محاسباتی داریم. و بعد با قرار دادن یک حلقه براحتی میتوانیم برای گام های زمانی بعدی اطلاعات بعدی را محاسبه نماییم.

نکته

همانطور که در تصویر مشاهده میکنید محاسبات مربوط به خروجی در تصویر نمایش داده نشده است و صرفا به نمایش یک خروجی به سافتمکس بسنده شده است. اگر بخواهیم این بخش را نیز در تصویر لحاظ کنیم با تصویر زیر مواجه خواهیم شد :

دلیل حذف این بخش صرفا برای جلوگیری از شلوغ شدن بیش از اندازه تصویر است. تصویر اول بعلت سادگی ,بهتر در حافظه شما باقی خواهد ماند و در ادامه وقتی که انواع جدیدتر را معرفی میکنیم این مساله خود را بهتر نشان خواهد داد.

حالا قصد داریم که فاز forward یک لایه RNN را آغاز کنیم. برای اینکار ابتدا خیلی ساده سعی میکنیم ساده ترین حالت ممکن را محاسبه کنیم . یعنی تابعی بنویسیم تا ورودی و حالت قبلی و همچنین پارامترهای مورد نیاز را دریافت کرده و بعد مقادیر جدید را محاسبه کند.


import numpy as np
from sklearn.utils.extmath import softmax

def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):
    """
        Here we run the forward pass for a single timestep of a vanilla RNN that uses a
        'tanh' activation function.
        The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the 
        hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.
        Inputs:
        - xt: Input data for this timestep, of shape (Batch_size, input_dim_size).
        - h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)
        - W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)
        - W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)
        - W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)
        - bh: Biases of shape (HiddenSize,)
        - bo: Biases of shape (output_dim_size,)
        
        Returns :
        - o_t: Output for the current timestep 
        - h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)
   """
    
    h_t = np.tanh(np.dot(xt, W1) + np.dot(h0, W2) + b_h)
    o_t = softmax(np.dot( h_t, W3.T) + b_o)
    return o_t, h_t

import numpy as np

from sklearn.utils.extmath import softmax

def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):

"""

Here we run the forward pass for a single timestep of a vanilla RNN that uses a

'tanh' activation function.

The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the

hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.

Inputs:

- xt: Input data for this timestep, of shape (Batch_size, input_dim_size).

- h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)

- W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)

- W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)

- W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)

- bh: Biases of shape (HiddenSize,)

- bo: Biases of shape (output_dim_size,)

Returns :

- o_t: Output for the current timestep

- h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)

"""

h_t = np.tanh(np.dot(xt, W1) + np.dot(h0, W2) + b_h)

o_t = softmax(np.dot( h_t, W3.T) + b_o)

return o_t, h_t

همانطور که در قطعه کد بالا توضیح داده شده است قصد ما پیاده سازی بخشی است که عملیات forward‌را به ازای یک گام زمانی انجام دهد. پیشتر ما روابط ریاضی حاکم بر این موضوع را مشاهده کردیم و حالا نیازمند جزییات بیشتری جهت پیاده سازی اصلی میباشیم. در گام اول ما نیازمند به یک تابع فعالسازی هستیم. یکی از توابع پراستفاده در این زمینه تابع tanh است ما نیز از این تابع برای پیشبرد هدف خود استفاده میکنیم. همچنین به منظور پیاده سازی بهینه تر این شبکه ما سعی میکنیم از موازی سازی تا حد امکان بهره ببریم. به همین منظور بجای یک قلم داده ورودی ما از یک دسته یا اصطلاحا mini batch بهره میبریم. یعنی ورودی xt ما شامل چند ورودی خواهد بود و ما در یک آن واحد خروجی های مورد نیاز را برای همه این ورودی ها محاسبه میکنیم.

علاوه بر ورودی ما نیازمند حالت مخفی قبلی(از مرحله یا گام زمانی قبل) نیز میباشیم. برای گام نخست چون هیچ گام زمانی قبلی ای وجود ندارد حالت مخفی ما صفر خواهد بود. حالت مخفی یک بردار با اندازه ای مشخص است که این اندازه یکی از فراپارامترهای مرتبط با کار با شبکه های عصبی بازگشتی است. اندازه این بردار(حالت مخفی) توسط ما مشخص میشود و در کد بصورت HiddenSize مشخص شده است. همانطور که پیشتر در تصاویر مرتبط با شبکه عصبی بازگشتی دیدیم وزنها و بایاسهایی نیز مورد نیاز هستند. از انجایی که این وزنها و بایاس ها برای همه گام های زمانی ثابت اند ما آنها را در قالب پارامترهای ورودی به تابع خود دریافت میکنیم.

ابعاد متغیرهای دخیل در کار ما به قرار زیر است :

-داده ورودی (xt) : داده ورودی برای گام زمانی فعلی : این متغییر دارای ابعاد (Batch_size, input_dim_size) میباشد. بُعد اول نمایانگر اندازه batch یا همان تعداد نمونه های ورودی بوده و بُعد دوم مشخص کننده ابعاد خود ورودی است. (در کاربرد متنی این اندازه برابر با اندازه لغت نامه ماست (ورودی ما در قالب یک بردار one-hot شده ارائه میشود).
-حالت مخفی یا حافظه (h0 یا $h_{previous }$ یا $h_{t-1}$ ) : حالت مخفی از گام زمانی قبلی : این متغییر دارای ابعاد (Batch_size, HiddenSize) میباشد. بُعد اول نمایانگر اندازه batch بوده و بُعد دوم مشخص کننده ابعاد خود حالت مخفی/حافظه است.(این عدد همان فراپارامتری است که صحبتش پیشتر رفت)

ماتریس وزن W1 : ماتریس وزن مختص ارتباطات بین ورودی-حالت مخفی: این متغییر دارای ابعاد (input_dim_size, HiddenSize) میباشد. بُعد اول نمایانگر اندازه داده ورودی بوده و بعد دوم نمایانگر اندازه حالت مخفی میباشد.

ماتریس وزن W2 : ماتریس وزن مختص ارتباطات بین حالت ورودی(قبلی) با حالت ورودی فعلی(بعدی): این متغییر دارای ابعاد (HiddenSize, HiddenSize) میباشد که هر دو بُعد اندازه حالت مخفی است.

ماتریس وزن W3 : ماتریس وزن مختص ارتباطات بین حالت مخفی(فعلی/بعدی) با خروجی: این متغییر دارای ابعاد (output_dim_size, hidden_state_size) میباشد. بُعد اول مشخص کننده اندازه (بردار) خروجی و بُعد دوم نمایانگر اندازه حالت مخفی است.

بردار bh : بایاس مرتبط با محاسبه حالت مخفی جدید : این متغییر دارای ابعاد (HiddenSize,) میباشد. به عبارت بهتر این بردار اندازه ای برابر با اندازه حالت مخفی دارد.

بردار bo : بایاس مرتبط با محاسبه خروجی : این متغییر دارای ابعاد (output_dim_size,) میباشد. به عبارت بهتر این بردار اندازه ای برابر با اندازه بردار خروجی دارد.

با مشخص شدن این ابعاد پیاده سازی محاسبات باقی مانده کار سختی نیست. ما از numpy استفاده میکنیم. numpy کتابخانه ای به زبان پایتون است که برای کار با آرایه های چند بعدی،بردارها ، ماتریس هاو … و همینطور انجام محاسبات ریاضی متنوع و گوناگون بر روی آنها است. اگر تجربه کار با متلب را دارید کار کردن با numpy برای شما بسیار آسان خواهد بود. در بخش منابع یادگیری سایت منبع بسیار خوبی جهت فراگیری این کتابخانه (و همینطور زبان پایتون) معرفی شده است که میتوانید با مراجعه به آن با این کتابخانه بشدت پرکاربرد زبان پایتون آشنا شوید.

برای ضرب ما از تابع dot کتابخانه numpy بهره میبریم و تنها نکته ای که در این رابطه باید بدانیم این است که سطر و ستون دو متغییر که قصد ضرب آنها را داریم با یکدیگر همخوانی داشته باشند.

نکته پیاده سازی :

در بعضی از پیاده سازی ها ممکن است مشاهده کنید که اندازه batch بجای بعد اول در بعد دوم قرار گرفته است. این کار به منظور ساده سازی محاسبات انجام میشود تا اینطور ابعاد ماتریس ها و بردارها بگونه ای در کنار هم قرار گیرند که عبارتی مثل W1.xt معتبر باشد.ذکر این نکته ضروری است که علاوه بر این تغییر ،جایگاه ابعاد در h0 نیز باید تغییر کند. چرا که h0 نیز در بعد اول خود دارای batchsize است. به همین ترتیب ابعاد W1 نیز باید جابجا شوند. ابعاد W1 از شکل (input_dim, hiddensize) به شکل (hiddensize, input_dim) تغییر میکند. بعد از انجام این کار میتوان براحتی نوشت np.dot(W1,xt) چرا که در اینجا ابعاد xt بصورت (input_dim, batchsize) بوده و ابعاد W1 نیز بصورت (hiddensize,input_dim) در آمده است در نتیجه ابعاد نزدیک بهم یکسان بوده و براحتی در یکدگیر ضرب میشوند. نکته مثبت این روش آن است که محاسبات به همان شکلی که در تصاویر مشاهده کردید قابل انجام بوده و اینگونه طبیعی تر بنظر می آیند. اما از طرفی بعلت جابجایی بُعد batch ممکن است عموما باعث ایجاد سردرگمی در تفسیر نتایج و پیاده سازی صحیح شبکه توسط دانشجویان شود. به همین علت محاسبات به شکلی که که مشاهده کردید انجام شده است. البته میتوان قبل انجام محاسبات تنها ابعاد این پارامترها را تغییر داده و بعد محاسبات را انجام داد. در اینصورت کد ما بصورت زیر خواهد بود :


import numpy as np
from sklearn.utils.extmath import softmax

def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):
    """
       Here we run the forward pass for a single timestep of a vanilla RNN that uses a
       'tanh' activation function.
       The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the 
       hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.
       Inputs:
       - xt: Input data for this timestep, of shape (Batch_size, input_dim_size).
       - h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)
       - W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)
       - W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)
       - W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)
       - bh: Biases of shape (HiddenSize,)
       - bo: Biases of shape (output_dim_size,)
       
       Returns :
       - o_t: Output for the current timestep 
       - h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)
    """
   
    # به منظور حفظ شکل محاسبات جای ابعاد را عوض میکنیم 
    xt = xt.transpose(1, 0)
    W1 = W1.transpose(1, 0)
    h0 = h0.transpose(1, 0)

    # در اینجا برای اینکه خطایی نگیریم لازم است ابعاد bh 
    # بجای  
    # (hiddensize,)
    #(hiddensize, 1) بصورت 
    h_t = np.tanh(np.dot(W1, xt) + np.dot(W2, h0) + bh.reshape(-1,1))
    # همین قضیه در مورد bo نیز صادق است 
    o_t = softmax(np.dot(W3, h_t) + bo.reshape(-1,1))
    
    return o_t, h_t

import numpy as np

from sklearn.utils.extmath import softmax

def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):

"""

Here we run the forward pass for a single timestep of a vanilla RNN that uses a

'tanh' activation function.

The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the

hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.

Inputs:

- xt: Input data for this timestep, of shape (Batch_size, input_dim_size).

- h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)

- W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)

- W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)

- W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)

- bh: Biases of shape (HiddenSize,)

- bo: Biases of shape (output_dim_size,)

Returns :

- o_t: Output for the current timestep

- h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)

"""

# به منظور حفظ شکل محاسبات جای ابعاد را عوض میکنیم

xt = xt.transpose(1, 0)

W1 = W1.transpose(1, 0)

h0 = h0.transpose(1, 0)

# در اینجا برای اینکه خطایی نگیریم لازم است ابعاد bh

# بجای

# (hiddensize,)

#(hiddensize, 1) بصورت

h_t = np.tanh(np.dot(W1, xt) + np.dot(W2, h0) + bh.reshape(-1,1))

# همین قضیه در مورد bo نیز صادق است

o_t = softmax(np.dot(W3, h_t) + bo.reshape(-1,1))

return o_t, h_t

حالا برای اینکه مطمئن شویم همه چیز بدرستی کار میکنید این قطعه از کد را بصورت زیر آزمایش میکنیم :


np.random.seed(1)

input_dim_size = 3
hidden_state_size = 5
output_size = 2
batch = 10

# W1 is multiplied by xt which has the shape (batch, input_dim_size)
W1 = np.random.randn(input_dim_size, hidden_state_size)
# W2 is multiplied by hidden_state, which has the shape h=(batchsize, hiddensize) 
# since w1 and w2 are added together, therefore, the dimension of h0.w2 
# must have the same shape of the result of xt.w1. 
W2 = np.random.randn(hidden_state_size, hidden_state_size)
# W3 is multiplied by hidden_state, and it should ultimately have the shape of input_dim_size
# h1.w3
W3 = np.random.randn(output_size, hidden_state_size)
# should have size of hidden_state_size
b_h = np.random.randn(hidden_state_size)
# should have size of outputsize
b_o = np.random.randn(output_size)

Xt = np.random.rand(batch, input_dim_size)
h0 = np.zeros(shape=(batch, hidden_state_size))

output, h_t = rnn_cell_forward(Xt, h0, W1, W2, W3, b_h, b_o)

print("h_t.shape = ", h_t.shape)
print("h_t[0] = ", h_t[0])
print("output.shape = ", output.shape)
print("output[0] =", output[0])

np.random.seed(1)

input_dim_size = 3

hidden_state_size = 5

output_size = 2

batch = 10

# W1 is multiplied by xt which has the shape (batch, input_dim_size)

W1 = np.random.randn(input_dim_size, hidden_state_size)

# W2 is multiplied by hidden_state, which has the shape h=(batchsize, hiddensize)

# since w1 and w2 are added together, therefore, the dimension of h0.w2

# must have the same shape of the result of xt.w1.

W2 = np.random.randn(hidden_state_size, hidden_state_size)

# W3 is multiplied by hidden_state, and it should ultimately have the shape of input_dim_size

# h1.w3

W3 = np.random.randn(output_size, hidden_state_size)

# should have size of hidden_state_size

b_h = np.random.randn(hidden_state_size)

# should have size of outputsize

b_o = np.random.randn(output_size)

Xt = np.random.rand(batch, input_dim_size)

h0 = np.zeros(shape=(batch, hidden_state_size))

output, h_t = rnn_cell_forward(Xt, h0, W1, W2, W3, b_h, b_o)

print("h_t.shape = ", h_t.shape)

print("h_t[0] = ", h_t[0])

print("output.shape = ", output.shape)

print("output[0] =", output[0])

و بعد از اجرای کد بالا با نتیجه زیر مواجه خواهیم شد:


h_t.shape =  (10, 5)
h_t[0] =  [ 0.8848139  -0.87440086 -0.98109225 -0.88240497  0.84867458]
output.shape =  (10, 2)
output[0] = [0.88185263 0.11814737]

h_t.shape = (10, 5)

h_t[0] = [ 0.8848139 -0.87440086 -0.98109225 -0.88240497 0.84867458]

output.shape = (10, 2)

output[0] = [0.88185263 0.11814737]

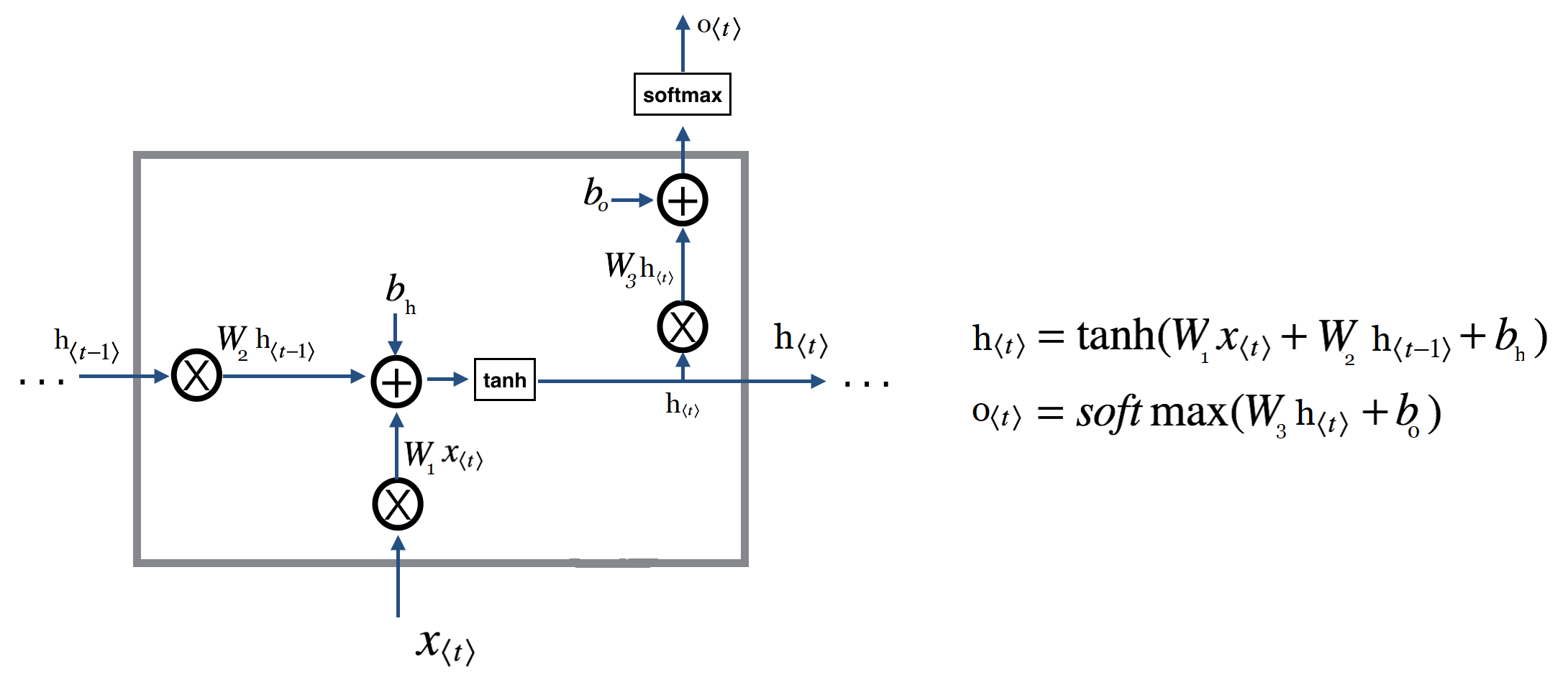
بعد از اینکه اطمینان حاصل کردیم قطعه کد اصلی ما بدرستی کار میکند نوبت به پیاده سازی بخش بعدی است. در این بخش هدف ما انجام این محاسبات به ازای گام های زمانی بیش از ۱ است. برای این مورد چه باید کرد؟ همانطور که پیشتر در این باره صحبت کردیم و در تصویر زیر نیز مشاهده میکنیم، عملیات های ما کماکان یکسان بوده اما این ورودی ها هستند که تغییر میکنند. بنابر این میتوانیم براحتی با استفاده از یک حلقه به این مساله رسیدگی کنیم :

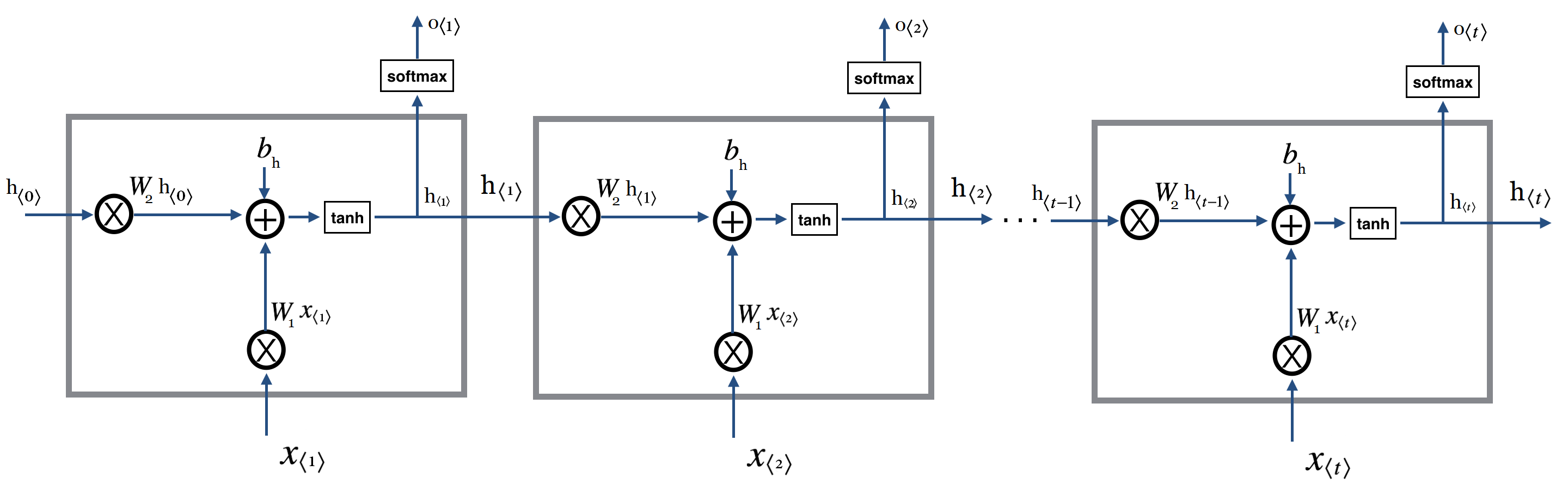اگر فرض کنیم که ورودی ما جمله ای مثل ” نام من حسین است” باشد به ترتیب هر کلمه بعنوان یک ورودی مورد استفاده قرار میگیرد. یعنی در گام زمانی اول کلمه “نام” تحت $X_1$ به لایه وارد میشود. در گام دوم این کلمه “من” است که در قالب ورودی $X_2$ وارد میشود. در گام زمانی سوم نیز “حسین” وارد میشود و به همین صورت الی آخر.(و اگر ورودی ما یک کلیپ ویدئویی باشد در گام زمانی اول فریم اول تحت نام $X_1$ به لایه وارد میشود. و به همین صورت سایر فریم ها در گام های زمانی همانند انچه در مورد جمله مشاهده کردیم مورد استفاد قرار میگیرند.) در همین حین به متغییر های $h$ توجه کنید. مشاهده میکنید که چگونه حالت قبلی در گام زمانی فعلی از مرحله قبل به مرحله فعلی (بعد) منتقل میشود.

پس با توجه به توضیحات بالا به این صورت عمل میکنیم :


def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o):
 
    """
        Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.
        We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)
        hidden_state_size: specifies the dimension of our h vectors(since we use a mini batch).
        W1, W2, W3, b_h and b_o are also parameters which we get as arguments.
    """
 
    batch, T_x, vocab_size = Xt.shape
    # for storing the results, we create two new variables. note that 
    # our variables, also have a new dimension, called T_x which essentially
    # specifies a timestep. 
    H = np.zeros(shape=(batch, T_x, hidden_state_size))
    O = np.zeros(shape=(batch, T_x, outputsize))
    h_previous = np.zeros(batch, hidden_state_size)
    
    for t in range(T_x): 
        output_t, h_t = rnn_cell_foward(Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)  
        O[:, t, :] = output_t
        H[:, t, :] = h_t
        # Our current/new hiddenstate will be the previous hiddenstate for the next round,
        h_previous = h_t 
        
    return O, H

def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o):

"""

Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.

We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)

hidden_state_size: specifies the dimension of our h vectors(since we use a mini batch).

W1, W2, W3, b_h and b_o are also parameters which we get as arguments.

"""

batch, T_x, vocab_size = Xt.shape

# for storing the results, we create two new variables. note that

# our variables, also have a new dimension, called T_x which essentially

# specifies a timestep.

H = np.zeros(shape=(batch, T_x, hidden_state_size))

O = np.zeros(shape=(batch, T_x, outputsize))

h_previous = np.zeros(batch, hidden_state_size)

for t in range(T_x):

output_t, h_t = rnn_cell_foward(Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)

O[:, t, :] = output_t

H[:, t, :] = h_t

# Our current/new hiddenstate will be the previous hiddenstate for the next round,

h_previous = h_t

return O, H

قائده کلی مشخص است. ما در یک حلقه که به تعداد گام های زمانی ماست در هر تکرار یک ورودی مختص به یک گام زمانی را مورد پردازش قرار میدهیم و حالت مخفی جدید و خروجی جدید (در صورت نیاز) را تولید میکنیم. این حالتها هر کدام ذخیره شده و سپس در گام بک پراپگیشن مورد استفاده قرار میگیرند.

یک نکته در رابطه با حالت مخفی اولیه یا همان $h_{t-1}$ یا همانطور که ما در قطعه کد بالا مشخص کرده ایم $h_{previous}$ وجود دارد. همانطور که در بالا مشاهده میکنید ما همیشه حالت اولیه را برداری از صفر در نظر میگیریم. اما همیشه اینگونه نیست که مقدار اولیه را بصورت برداری از صفر در نظر بگیریم . در بسیاری از کاربردها خصوصا در زمانی که ارتباط بین نمونه های ورودی وجود داشته باشد ما از اخرین حالت مخفی نمونه قبل بعنوان حالت اولیه نمونه فعلی(بعد) استفاده میکنیم. بعبارت بهتر اگر در حال حاضر شیوه فراخوانی ما بصورت زیر باشد :


for i in range (iterations): 
    Xt = get_new_samples(i)
    O, H = rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o)
    ....

for i in range (iterations):

Xt = get_new_samples(i)

O, H = rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o)

....

بعد از اعمال تغییرات بصورت زیر خواهد بود :


# defining the initial hiddenstate
h_previous = np.zeros(batch_size, hidden_state_size)

for i in range (iterations): 
    Xt = get_new_samples(i)
    O, H = rnn_layer_forward(Xt, h_previous, W1, W2, W3, b_h, b_o)
    # get the last hiddenstate and use it as the previous hidden state(initia hidden state) for
    # the next set of examples. 
    h_previous = H[:,-1,:]

# defining the initial hiddenstate

h_previous = np.zeros(batch_size, hidden_state_size)

for i in range (iterations):

Xt = get_new_samples(i)

O, H = rnn_layer_forward(Xt, h_previous, W1, W2, W3, b_h, b_o)

# get the last hiddenstate and use it as the previous hidden state(initia hidden state) for

# the next set of examples.

h_previous = H[:,-1,:]

همانطور که در کد بالا مشاهده میکنیم در ابتدای آموزش ما از بردار صفر استفاده کرده اما در ادامه این مقدار اولیه برای نمونه های بعدی از آخرین حالت مخفی که از نمونه قبل بدست امده است بهره میبرد. در نتیجه میتوان کد را بصورت زیر تغییر داد تا هر دو حالت را بتوان مورد استفاده قرار داد :


def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o, h_previous=None):
    """
        Xt: Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.
            We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)
        h_previous: The initial hidden state. if set to None, we will always use vector of zeros as initial hidden state
        W1, W2, W3, b_h and b_o are also parameters which we get as arguments.
    """

    batch, T_x, vocab_size = Xt.shape
    # for storing the results, we create two new variables. note that
    # our variables, also have a new dimension, called T_x which essentially
    # specifies a timestep.
    H = np.zeros(shape=(batch, T_x, hidden_state_size))
    O = np.zeros(shape=(batch, T_x, outputsize))

    if h_previous is None:
        h_previous = np.zeros(shape=(batch, hidden_state_size))

    for t in range(T_x):
        output_t, h_t = rnn_cell_forward( Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)
        O[:, t, :] = output_t
        H[:, t, :] = h_t
        # Our current/new hiddenstate will be the previous hiddenstate for the next round,
        h_previous = h_t

    return O, H

def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o, h_previous=None):

"""

Xt: Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.

We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)

h_previous: The initial hidden state. if set to None, we will always use vector of zeros as initial hidden state

W1, W2, W3, b_h and b_o are also parameters which we get as arguments.

"""

batch, T_x, vocab_size = Xt.shape

# for storing the results, we create two new variables. note that

# our variables, also have a new dimension, called T_x which essentially

# specifies a timestep.

H = np.zeros(shape=(batch, T_x, hidden_state_size))

O = np.zeros(shape=(batch, T_x, outputsize))

if h_previous is None:

h_previous = np.zeros(shape=(batch, hidden_state_size))

for t in range(T_x):

output_t, h_t = rnn_cell_forward( Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)

O[:, t, :] = output_t

H[:, t, :] = h_t

# Our current/new hiddenstate will be the previous hiddenstate for the next round,

h_previous = h_t

return O, H

برای اینکه از کارکرد درست پیاده سازی تا به اینجا مطمئن شویم کدها را بصورت زیر آزمایش میکنیم :


import numpy as np

from sklearn.utils.extmath import softmax


def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):
    """
        Here we run the forward pass for a single timestep of a vanilla RNN that uses a
        'tanh' activation function.
        The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the 
        hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.
        Inputs:
        - xt: Input data for this timestep, of shape (Batch_size, input_dim_size).
        - h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)
        - W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)
        - W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)
        - W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)
        - bh: Biases of shape (HiddenSize,)
        - bo: Biases of shape (output_dim_size,)

        Returns :
        - o_t: Output for the current timestep 
        - h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)
   """

    h_t = np.tanh(np.dot(xt, W1) + np.dot(h0, W2) + b_h)
    o_t = softmax(np.dot(h_t, W3.T) + b_o)
    return o_t, h_t


def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o, h_previous=None):
    """
        Xt: Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.
            We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)
        h_previous: The initial hidden state. if set to None, we will always use vector of zeros as initial hidden state
        W1, W2, W3, b_h and b_o are also parameters which we get as arguments.
    """

    batch, T_x, vocab_size = Xt.shape
    # for storing the results, we create two new variables. note that
    # our variables, also have a new dimension, called T_x which essentially
    # specifies a timestep.
    H = np.zeros(shape=(batch, T_x, hidden_state_size))
    O = np.zeros(shape=(batch, T_x, outputsize))

    if h_previous == None:
        h_previous = np.zeros(shape=(batch, hidden_state_size))

    for t in range(T_x):
        output_t, h_t = rnn_cell_forward( Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)
        O[:, t, :] = output_t
        H[:, t, :] = h_t
        # Our current/new hiddenstate will be the previous hiddenstate for the next round,
        h_previous = h_t

    return O, H


np.random.seed(1)
input_dim_size = 3
hidden_state_size = 5
outputsize = 3
batch = 2
timesteps = 4

W1 = np.random.randn(input_dim_size, hidden_state_size)
W2 = np.random.randn(hidden_state_size, hidden_state_size)
W3 = np.random.randn(outputsize, hidden_state_size)
bh = np.random.randn(hidden_state_size)
bo = np.random.randn(outputsize)


Xt = np.random.rand(batch, timesteps, input_dim_size)
h_previous = np.zeros(shape=(batch, hidden_state_size))

Outputs, HiddenStates = rnn_layer_forward( Xt, hidden_state_size, W1, W2, W3, bh, bo)


print('W1: ', W1.shape)
print('W2: ', W2.shape)
print('W3: ', W3.shape)
print('bh: ', bh.shape)
print('bo: ', bo.shape)

print("HiddenStates.shape = ", HiddenStates.shape)
print("HiddenStates[0] = ", HiddenStates[0])
print("Outputs.shape = ", Outputs.shape)
print("Outputs[0] =", Outputs[0])

import numpy as np

from sklearn.utils.extmath import softmax

def rnn_cell_forward(xt, h0, W1, W2, W3, b_h, b_o):

"""

Here we run the forward pass for a single timestep of a vanilla RNN that uses a

'tanh' activation function.

The input data has dimension input_dim_size(vocabulary size in case we have nlp use), the

hidden state has dimension 'HiddenSize', and we use a minibatch size of 'Batch_size'.

Inputs:

- xt: Input data for this timestep, of shape (Batch_size, input_dim_size).

- h0(or also known as h_previous): Hidden state from previous timestep, of shape (Batch_size, HiddenSize)

- W1: Weight matrix for input-to-hidden connections, of shape (input_dim_size, HiddenSize)

- W2: Weight matrix for hidden-to-hidden connections, of shape (HiddenSize, HiddenSize)

- W3: Weight matrix for hiddent-to-output connections, of shape(output_dim_size, hidden_state_size)

- bh: Biases of shape (HiddenSize,)

- bo: Biases of shape (output_dim_size,)

Returns :

- o_t: Output for the current timestep

- h_t(or also known as h_next): Next hidden state, of shape (Bachsize, HiddenSize)

"""

h_t = np.tanh(np.dot(xt, W1) + np.dot(h0, W2) + b_h)

o_t = softmax(np.dot(h_t, W3.T) + b_o)

return o_t, h_t

def rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3, b_h, b_o, h_previous=None):

"""

Xt: Since we have our input(Xt), we can infer all of the info concerning the shape, timesteps, etc.

We suppose our input has the shape ( batch, Tx_number_of_Time_steps, vocab_size)

h_previous: The initial hidden state. if set to None, we will always use vector of zeros as initial hidden state

W1, W2, W3, b_h and b_o are also parameters which we get as arguments.

"""

batch, T_x, vocab_size = Xt.shape

# for storing the results, we create two new variables. note that

# our variables, also have a new dimension, called T_x which essentially

# specifies a timestep.

H = np.zeros(shape=(batch, T_x, hidden_state_size))

O = np.zeros(shape=(batch, T_x, outputsize))

if h_previous == None:

h_previous = np.zeros(shape=(batch, hidden_state_size))

for t in range(T_x):

output_t, h_t = rnn_cell_forward( Xt[:, t, :], h_previous, W1, W2, W3, b_h, b_o)

O[:, t, :] = output_t

H[:, t, :] = h_t

# Our current/new hiddenstate will be the previous hiddenstate for the next round,

h_previous = h_t

return O, H

np.random.seed(1)

input_dim_size = 3

hidden_state_size = 5

outputsize = 3

batch = 2

timesteps = 4

W1 = np.random.randn(input_dim_size, hidden_state_size)

W2 = np.random.randn(hidden_state_size, hidden_state_size)

W3 = np.random.randn(outputsize, hidden_state_size)

bh = np.random.randn(hidden_state_size)

bo = np.random.randn(outputsize)

Xt = np.random.rand(batch, timesteps, input_dim_size)

h_previous = np.zeros(shape=(batch, hidden_state_size))

Outputs, HiddenStates = rnn_layer_forward( Xt, hidden_state_size, W1, W2, W3, bh, bo)

print('W1: ', W1.shape)

print('W2: ', W2.shape)

print('W3: ', W3.shape)

print('bh: ', bh.shape)

print('bo: ', bo.shape)

print("HiddenStates.shape = ", HiddenStates.shape)

print("HiddenStates[0] = ", HiddenStates[0])

print("Outputs.shape = ", Outputs.shape)

print("Outputs[0] =", Outputs[0])

خروجی :


W1:  (3, 5)
W2:  (5, 5)
W3:  (3, 5)
bh:  (5,)
bo:  (3,)
HiddenStates.shape =  (2, 4, 5)
HiddenStates[0] =  [[ 0.03138719  0.71325441 -0.23865882 -0.120134    0.94330192]
                    [ 0.97244455 -0.89825603  0.8744728   0.88125945  0.99897104]
                    [-0.61569448 -0.9665565  -0.99155636  0.09897279  0.96139953]
                    [ 0.96862788 -0.71801066  0.59641631  0.87758927  0.38586669]]
Outputs.shape =  (2, 4, 3)
Outputs[0] = [[0.04281752 0.70848249 0.24869999]
              [0.09045469 0.88060607 0.02893924]
              [0.36031291 0.10900506 0.53068203]
              [0.18948049 0.72264519 0.08787432]]

W1: (3, 5)

W2: (5, 5)

W3: (3, 5)

bh: (5,)

bo: (3,)

HiddenStates.shape = (2, 4, 5)

HiddenStates[0] = [[ 0.03138719 0.71325441 -0.23865882 -0.120134 0.94330192]

[ 0.97244455 -0.89825603 0.8744728 0.88125945 0.99897104]

[-0.61569448 -0.9665565 -0.99155636 0.09897279 0.96139953]

[ 0.96862788 -0.71801066 0.59641631 0.87758927 0.38586669]]

Outputs.shape = (2, 4, 3)

Outputs[0] = [[0.04281752 0.70848249 0.24869999]

[0.09045469 0.88060607 0.02893924]

[0.36031291 0.10900506 0.53068203]

[0.18948049 0.72264519 0.08787432]]

در بخش سوم به پیاده سازی Back-propagation in time خواهیم پرداخت و بعد از آن به توضیحات GRU و LSTM خواهیم پرداخت. سپس با استفاده از پیاده سازی ای که در اینجا انجام دادیم مثالهای مختلفی را با استفاده از این پیاده سازی اجرا خواهیم کرد.

13 نظرات

آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش اول | یادگیری عمیق - Deep learning 5 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش دوم […]
آموزش شبکه عصبی بازگشتی بخش چهارم : معرفی GRU | یادگیری عمیق - Deep learning 5 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش دوم : Forwa… […]
آموزش شبکه عصبی بازگشتی بخش پنجم : معرفی LSTM | یادگیری عمیق - Deep learning 5 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش دوم : Forwa… […]
آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش اول | یادگیری عمیق - Deep learning 5 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent Neural Networks) بخش دوم : Forwa… […]
مهسا می گوید 5 سال پیش

ببینید بر فرض مثال من بخوام دو جمله به این شبکه بدهم که هر جملش سه کلمه داره یعنی batch=2,input_dim_size=3
[نام من حسین؛نام او علی]=xt
هست حالا اگر مثلا timesteps=4 باشه
الان من متوجه نمیشم
Xt = (batch, timesteps, input_dim_size)یعنی چی میشه؟ و مثلا در تایم استپ اول چی میگیره؟

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  سلام.
  اون سه کلمه ای که شما مشخص میکنید در اصل اندازه تایم استپ شماست . ابعاد ورودی شما(و همینطور خروجی شما) در قالب بردار One hot ارائه میشه و اون dim_size یی که مینویسیم اشاره به ابعاد بردار وان هات شده است.
  ایده اینه که در هر گام زمانی یک کلمه ارائه میشه. اگر جمله شما ۳ کلمه باشه یعنی سه گام زمانی داریم.
  
  پاسخ
مهسا می گوید 5 سال پیش

بر فرض مثال روی همین اعدادی که خودتون کدش زدید
الان batch=2 این یعنی دو جمله درسته؟
time step=4 یعنی هر جمله چهار کلمه داره درسته؟ وباید چهار گام زمانی حلقه جلو بره؟
Ali , Maryam]
See , watch
His , tv
Friend, program]
خب وقتی وارد حلقه میشه اولین T_x=0 هست یعنی [:,۰,:]=xt
مگه منظور سطر صفرم همه ستون ها نیست؟ و این میشه ali maryam درسته؟پس این دو اسم به عنوان دو وردی در اولین گام زمانی میگیره؟ که هر کدوم سه سطر دارند یعنی (۲,۳) که هرسطر یک onehot درسته؟
که این ۳ همونinput_dim_size=3 ؟

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  ابعاد ورودی شما وابسته به اندازه لغت نامه شماست. وقتی شما میخوایید بردار One hot شده از یک کلمه رو بسازید اون رو بر اساس لغت نامه خودتون ایجاد میکنید. (مثلا یک متنی دارید که درش ۲۰ تا کلمه یکتا وجود داره. حالا شما میایید یک بردار ایجاد میکنید به اندازه ۲۰ و هر کلمه رو به یک اندیس این بردار اختصاص میدید. دقت کنید ممکنه متن شما ۵۰ هزار کلمه داشته باشه اما این ۵۰ هزار همون ۲۰ تا کلمه یکتا هستن که تکرار شدند!)
  برای مثال شما فرض کنید لغت نامه ما کلا ۸ کلمه ای باشه (مثلا فقط ۸ تا کلمه داریم که ۴ تاش تو جمله مریم استفاده شده و ۴ تاش هم در جمله علی!) در این صورت مریم مثلا بصورت ۰۱۰۰۰۰۰۰ علی بصورت ۱۰۰۰۰۰۰۰ see بصورت ۰۰۱۰۰۰۰۰ ,و همینطور الی اخر کد خواهد شد.
  پس input_dim_size شما برابر با ۸ هست (اندازه لغت نامه شما!) وقتی میگیم در گام زمانی ۰ یعنی
  اگر batch = 1 در نظر بگیریم بردار ورودی
  میشه بردار مریم که میشه ۰۱۰۰۰۰۰۰
  [۰۱۰۰۰۰۰]
  اگر batch=2 باشه. بردار علی هم (که مربوط به نمونه دیگری هست) اضافه میشه :
  [۰۱۰۰۰۰۰۰]]
  [[۱۰۰۰۰۰۰۰],
  در گام زمانی بعدی نوبت به کلمات بعدی در جمله ما میرسه . یعنی watch و see . پس ورودی ما با بچ =۲ مثلا بصورت زیر میشه :
  [۰۰۱۰۰۰۰۰]]
  [[۰۰۰۱۰۰۰۰],
  و همینطور الی آخر
  
  پس در اینجا اندازه لغت نامه ما برابر با ۸ هست (فرض کردیم فقط همین ۸ تا کلمه که در دو جمله مثال زدیم وجود داره).
  اندازه گام زمانی ما برابر با ۴ هست (چون هر جمله ۴ کلمه داره)
  و اندازه ورودی ما هم برابر با ۸ هست (به همون اندازه لغت نامه ما)
  اگر بخواهیم ابعاد رو بفرم numpy (یا ماتریسی ) نمایش بدیم میشه ۲x4x8
  اولی مشخص کننده اندازه بچ ماست. دومی تعداد گام های زمانی و سومی ابعاد هر کلمه ما.
  
  پاسخ
مهسا می گوید 5 سال پیش

تشکر از توضیحاتتون.

پاسخ
سهراب می گوید 5 سال پیش

با سلام خدمت آقای حسن پور . ممنون از مقالات خوبتون.
پایین نکته پیاده سازی همانجا که اولین تست را ذکر کرده اید خروجی output[0] بنده با آنچه شما نوشته اید تفاوت دارد . من تنها کد را کپی پیست کردم . ممنون.
خروجی من بصورت :
(‘output.shape = ‘, (10, 2))
(‘output[0] =’, array([0.88185263, 0.11814737]))
و آنچه شما نوشته اید به صورت زیر است:
output.shape = (10, 2)
output[0] = [0.09485435 0.06592572]
با تشکر.

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  سلام
  خروجی که شما میگیرید صحیحه. این خروجی از نسخه اول باقی مونده بود که از قرار معلوم بروز نکرده بودم. تصحیح شد.
  برای تست میتونید از اینجا استفاده کنید.
  خیلی ممنونم از شما.
  
  پاسخ
رحمان می گوید 5 سال پیش

عالی بود.
بسیار شفاف توضیح دادین
ممنون

پاسخ
Hediyeh می گوید 3 سال پیش

خیلی تشکر از مطالب بسیار عالی و مفیدتون. امیدوارم کائنات خوشبختی رو به سمت شما روانه کنه

پاسخ

ارسال یک پاسخ

این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش می‌شوند.