آموزش شبکه های عصبی بازگشتی (Recurrent neural network) بخش سوم : Backpropagation

توسط سید حسین حسن پور متی کلایی در مارس 26, 2019 آخرین بروزرسانی اکتبر 13, 2019

بسم الله الرحمن الرحیم

در بخش قبل(بخش دوم) با هم چگونگی پیاده سازی فاز پیشرو (forward pass) در یک شبکه عصبی بازگشتی (Recurrent Neural network) را به انجام رساندیم. در این پست به فاز دوم پیاده سازی یعنی پیاده سازی عملیات پس انتشار (Backpropagation) در یک شبکه عصبی بازگشتی خواهیم پرداخت.

در این بخش با مفاهیم “پس انتشار در زمان” و “پس انتشار کوتاه” شده نیز آشنا خواهیم شد.

حالا نوبت به پیاده سازی بخش پس انتشار است. اما قبل از انکه ادامه دهیم اجازه دهید با هم مروری بر این فرآیند داشته باشیم و ببینیم چگونه باید به پیش برویم .

عملیاتهای صورت گرفته در بخش forward مشخص هستند اما برای اینکه قادر باشیم این فاز را بدرستی پیاده سازی کنیم نیاز به جزییات بیشتری داریم . میدانیم که در یک شبکه RNN ما بطور خاص با یک حلقه سرو کار داریم به همین جهت گرادیان هایی که به ازای عملیات انجام شده بدست می آوریم را بایستی با هم جمع کنیم تا در نهایت بدرستی تاثیرات صورت گرفته در فاز forward را لحاظ کرده باشیم .

همانطور که بالا دیدیم فاز forward ما متشکل از ۲ عملیات کلی بود که به قرار زیراند :

$h_t = tanh(W_1 \cdot X_t +W_2 \cdot h_{t-1} + b_h)$

$o_t = softmax(W_3 \cdot h_t + b_o)$

برای انجام پس انتشار ما از گام زمانی اخر شروع کرده خطا را محاسبه میکنیم و سپس در یک حلقه محاسبات را به ازای تمامی گام های زمانی ادامه میدهیم .

فرض ما در اینجا این است که شما با عملیات پس انتشار(backpropagation) آشنایید بنابر این در اینجا با جزییات کامل پس انتشار(که پس انتشار چیست) آشنا نمیشویم انشاءالله در مورد عملیات پس انتشار و مبحث گرادیان ها در مطلبی جداگانه بطور مفصل صحبت خواهم کرد اما بطور کوتاه باید بدانیم که الگوریتم پس انتشار (خطا) یک الگوریتم credit assignment است. یعنی کار این الگوریتم منتسب کردن پاداش یا جزای هر پارامتر نسبت به نتیجه بدست امده نهایی است. اینکه هر پارامتر چقدر در نتیجه بدست امده دخیل بوده و در صورت نتیجه صحیح و یا غلط به چه میزان بایستی تغییر کند. این تمام چیزی است که این الگوریتم مسئولیت انجام آن را دارد. ستون فقرات این الگوریتم را هم گرادیان ها تشکیل میدهند. کاری که ما در اینجا بایستی انجام دهیم مشخص کردن میزان تاثیر هرکدام از متغییرها بر روی نتیجه بدست آمده نهایی است. برای اینکار ما از مشتق جزئی استفاده میکنیم همانطور که حتما میدانید مشتق جزئی در مورد توابع چند متغیره، به مشتق تابع نسبت به یکی از متغیرها با ثابت نگه‌داشتن سایر متغیرها گفته می‌شود. بعنوان مثال در عبارت $f(x,y) = 3x^2 + 5xy - 2y^4$ مشتق جزئی $f$ نسبت به $x$ برابر با $6x + 5y$ خواهد بود. و اگر از تابع $f$ نسبت به $y$ بخواهیم مشتق بگیریم نتیجه برابر با $5x - 8y^3$ خواهد بود. زمانی که با مشتق جزئی سرو کار داریم از نماد $\partial$ استفاده میکنیم. برای یادآوری این مبحث میتوانید به این نوشته کوتاه و بسیار خوب مراجعه کنید.

خب به بحث اصلی برگردیم. برای محاسبه گرادیان ها ما بصورت زیر بایستی عمل کنیم :

محاسبه خطا : $output_t - label_t$
محاسبه گرادیان عبارت خروجی : $o_t = softmax(W_3 \cdot h_t + b_o)$
محاسبه گرادیان عبارت مربوط به حالت مخفی جدید : $h_t = tanh(W_1 \cdot X_t +W_2 \cdot h_{t-1} + b_h)$

ابتدا سعی میکنیم خطا را محاسبه کرده و سپس مشتق جزئی برای رابطه $o_t = softmax(W_3 \cdot h_t + b_o)$ را بدست بیاوریم .

برای محاسبه مشتق عبارت فوق بهتر است از فرم ساده شده آن استفاده کنیم تا فرآیند مشتق گیری آسان تر باشد. ما میتوانیم تابع فوق را بصورت $o = f(W_3.h + b_o)$ در نظر بگیریم. بعد از اینکار مشتق ما بصورت زیر خواهد بود :

$dW_3 = h.du$

$dh = W_3.du$

$db_o = 1.du$

از انجایی که در این بخش ما بصورت مستقیم با خطا در ارتباط هستیم در نتیجه خطا را بصورت مستقیم میتوانیم لحاظ کنیم بنابر این خواهیم داشت :

$dW_3 = h.error$

$dh = W_3.error$

$db_o = 1.error$

پیاده سازی این عبارات در پایتون بصورت زیر خواهد بود :


# must have the shape of W3 which is (output_dim_size, hidden_state_size)
dW3 = np.dot(e.T, h)
dh = np.dot(e, W3)   
# dbo =e.1, since we have batch we use np.sum 
# e is a vector, when it is subtracted from label, the result will be added to dbo
dbo = np.sum(e, axis=0)

# must have the shape of W3 which is (output_dim_size, hidden_state_size)

dW3 = np.dot(e.T, h)

dh = np.dot(e, W3)

# dbo =e.1, since we have batch we use np.sum

# e is a vector, when it is subtracted from label, the result will be added to dbo

dbo = np.sum(e, axis=0)

نکته:

در تعاریف بالا یک مشکل وجود دارد و آن بحث لحاظ کردن حالات مخفی و تاثیرات آنها بر یکدیگر است . همانطور که در فاز forward حالت قبلی در گام زمانی بعدی مورد استفاده قرار میگرفت به همین صورت نیز مشتق حالت مخفی از گام زمانی جدیدتر به گام زمانی قدیمی تر بایستی منتقل شود. از آنجایی که در فاز پس انتشار ما از اخرین گام زمانی شروع کرده و بعد از این گام زمانی دیگری وجود ندارد در نتیجه در شروع کار $\partial h$ = ۰ خواهد بود. اما این مقدار هر بار بروز شده و در گام زمانی قبل تر مورد استفاده قرار میگیرد.

همانطور که در تصویر زیر میبینیم هر سلول $h$ فعلی را به گام زمانی بعدی ارسال میکند. به همین صورت در زمان بک پراپگیشن هم $\partial h$ علاوه بر محاسبه گرادیان مبتنی بر خروجی ، گرادیان حاصل از گام زمانی بعدی نیز بایستی لحاظ شود.

در تصویر زیر این مهم مشخص شده است, نکته قابل اهمیت dh است به همین منظور تنها جهت جریان forward و همینطور گرادیان متناظر با آن مشخص شده است .

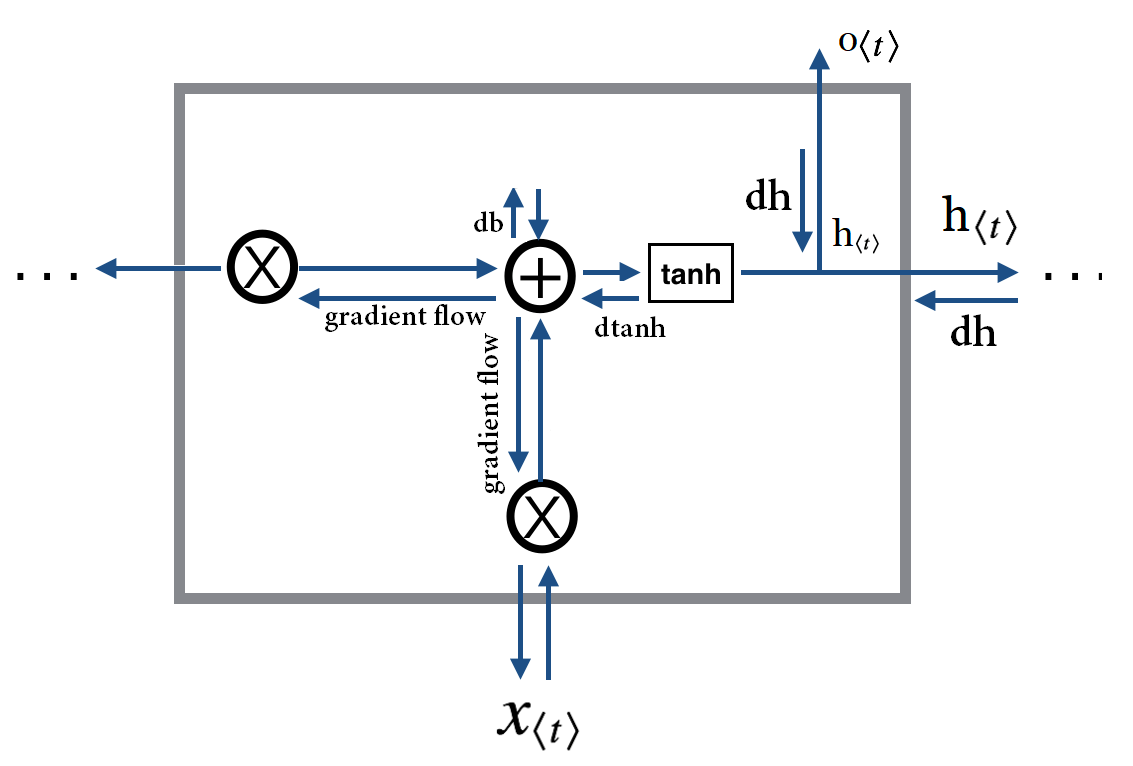
به همین خاطرمحاسبه $dh$ بصورت زیر خواهد بود :

*** QuickLaTeX cannot compile formula:
dh = W_3.error + dh_{from\_next\_timestep}}

*** Error message:
Extra }, or forgotten $.
leading text: $dh = W_3.error + dh_{from\_next\_timestep}}

و از انجایی که شروع عملیات پس انتشار از گام زمانی اخر است و گام زمانی بعدی وجود ندارد مقدار $dh_{from\_next\_timestep}$ در ابتدا صفر میباشد.

به همین صورت پیاده سازی عبارات فوق در زبان پایتون بصورت زیر خواهند بود :


# must have the shape of W3 which is (output_dim_size, hidden_state_size)
dW3 = np.dot(e.T, h)
# when calculating the dh, we also add the dh from the next timestep as well
# when we are in the last timestep, the h_gradient_or_dh is initially zero.
dh = np.dot(e, W3) + h_gradient_or_dh  
# dbo =e.1, since we have batch we use np.sum 
# e is a vector, when it is subtracted from label, the result will be added to dbo
dbo = np.sum(e, axis=0)

# must have the shape of W3 which is (output_dim_size, hidden_state_size)

dW3 = np.dot(e.T, h)

# when calculating the dh, we also add the dh from the next timestep as well

# when we are in the last timestep, the h_gradient_or_dh is initially zero.

dh = np.dot(e, W3) + h_gradient_or_dh

# dbo =e.1, since we have batch we use np.sum

# e is a vector, when it is subtracted from label, the result will be added to dbo

dbo = np.sum(e, axis=0)

حالا نیازمند محاسبه مشتقات جزئی برای عبارت دوم هستیم . همانطور که تازه دیدیم میتوانیم این عبارت را نیز بصورت $h = f(u)$ ساده سازی کنیم. از انجایی که تابع $f$ ما در اینجا در اصل $tanh$ است و مشتق $tanh(u)$ برابر با

*** QuickLaTeX cannot compile formula:
1-tan(u)^2\partialu

*** Error message:
Undefined control sequence \partialu.
leading text: $1-tan(u)^2\partialu

است. بنابر این خواهیم داشت $h = tanh(u)$ و با جایگزین کردن خواهیم داشت:

$dtanh = (1-h^2)\partial h$

چرا که

$h = tanh(u)$

*** QuickLaTeX cannot compile formula:
dtanh = (1-tanh(u)^2\partialu)

*** Error message:
Undefined control sequence \partialu.
leading text: $dtanh = (1-tanh(u)^2\partialu

پس

$( 1 - tanh(u)^2.du ) == ( 1 - h^2.dh )$

به همین صورت مشتق سایر عبارتها را بصورت زیر بدست می آوریم :

$dX_t = W_1.dtanh$
$dW_1 = X_t.dtanh$
$dW_2 = h_{prev}.dtanh$
$db_h = 1.dtanh$

حالا اگر بخواهیم معادل این دستورات را در پایتون داشته باشیم بصورت زیر عمل میکنیم.

توجه :

دقت کنید که ما در اینجا ضرب بین بردارها و ماتریس ها را داریم و ابعاد مشتقات برابر با اندازه بردار یا ماتریس متناظر آن است(همانطور که قبلا گفتیم در مشتق ما بدنبال میزان تاثیر هر “پارامتر” بر روی نتیجه نهایی هستیم. پس به ازای هر پارامتر قابل یادگیری (هر دارایه ماتریس یا بردار) ما یک مقدار خواهیم داشت. همینطور توجه کنید که ما تنها به پارامترهای قابل ترین اهمیت میدهیم.(کد زیر را ببینید)


    # the input part
    dtanh = (1 - h * h) * dh
 
    # compute the gradient of the loss with respect to W1
	# this is actually not needed!, because its not a tunable parameter!
    # dxt = np.dot(dtanh, W1.T) 
    # must have the shape of (input_dim_size, hidden_state_size)
    dW1 = np.dot(xt.T, dtanh)
 
    # compute the gradient with respect to W2
    dh_prev = np.dot(dtanh, W2.T)
    # shape must be (HiddenSize, HiddenSize)
    dW2 = np.dot(h_prev.T, dtanh)
 
    # dbh += dtanh.1, we use sum, since we have a batch
    dbh = np.sum(dtanh, axis=0)

# the input part

dtanh = (1 - h * h) * dh

# compute the gradient of the loss with respect to W1

# this is actually not needed!, because its not a tunable parameter!

# dxt = np.dot(dtanh, W1.T)

# must have the shape of (input_dim_size, hidden_state_size)

dW1 = np.dot(xt.T, dtanh)

# compute the gradient with respect to W2

dh_prev = np.dot(dtanh, W2.T)

# shape must be (HiddenSize, HiddenSize)

dW2 = np.dot(h_prev.T, dtanh)

# dbh += dtanh.1, we use sum, since we have a batch

dbh = np.sum(dtanh, axis=0)

بعد از مشخص کردن موارد بالا پیاده سازی کامل این فاز براحتی قابل انجام خواهد بود. دو تابع زیر وظیفه پیاده سازی موارد مطرحی بالا را بعهده دارند :


def rnn_cell_backward(xt,
                        h,
                        h_prev,
                        output,
                        true_label,
                        h_gradient_or_dh,
                        W1,
                        W2,
                        W3 ):
    """
       xt:   
          is the input in the form of (batch_size, input_dim_size)
       h :   
          is the next hidden state
       h_prev: 
          is the previous hidden state 
       output: 
          is the output of the rnn cell!
       true_label: 
          is the true label for the current output
    h_gradient_or_dh: 
			The dh which in the beginning is zero
			and is updated as we go backward in the backprogagation.
			the dh for the next round, would come from the dh_prev.
			remember the backward pass is essentially a loop! and we
			start at the end and traverse back to the beginning!
    """

    e = np.copy(output)
    
	# This is error_t = output_t - label_t
	e[np.arange(e.shape[0]), np.argmax(true_label, axis=1)] -=1
    # This is used for our loss to see how well we are doing during training.
	per_ts_loss = output[np.arange(output.shape[0]), np.argmax(true_label, axis=1)].sum()
	
    # this is the non-vectorized version of the above snippet
	# per_ts_loss = 0
    # for i, idx in enumerate(np.argmax(true_label, axis=1)):
        # e[i, idx] -=1
        # per_ts_loss += output[i, idx]    

	dW3 = np.dot(e.T, h)
	# when calculating the dh, we also add the dh from the next timestep as well
	# when we are in the last timestep, the h_gradient_or_dh is initially zero.
	dh = np.dot(e, W3) + h_gradient_or_dh  
	# dbo = e.1, since we have batch we use np.sum 
	# e is a vector, when it is subtracted from label, the result will be added to dbo
	dbo = np.sum(e, axis=0)

	
    # the input part
    dtanh = (1 - h * h) * dh
 
    # compute the gradient of the loss with respect to W1
	# this is actually not needed! bcause Xt is not a tunable
	# parameter, thererfore we dont need it gradient. 
    # dxt = np.dot(dtanh, W1.T) 
	
    # must have the shape of (input_dim_size, hidden_state_size)	
    dW1 = np.dot(xt.T, dtanh)
 
    # compute the gradient with respect to W2
    dh_prev = np.dot(dtanh, W2.T)
    # shape must be (HiddenSize, HiddenSize)
    dW2 = np.dot(h_prev.T, dtanh)
 
    # dbh += dtanh.1, we use sum, since we have a batch
    dbh = np.sum(dtanh, axis=0)

    return dW1, dW2, dW3, dbh, dbo, dh_prev, per_ts_loss


def rnn_layer_backward( Xt,
                        labels,
                        H,
                        O,
                        W1,
                        W2,
                        W3,
                        bh,
                        bo ):
	"""
	   Xt: 			
			The input in the form of (batch_size, time-step, input_dim_size)
	   labels:		
			The labels for each output with the shape (batch_size, time-step, outputsize)
       H :      	
			All the hidden states from the forward pass with the shape (batch_size, time-step, hidden_state_size)
       O:       	
			All the outputs from the forward pass 

	   W1,W2,W3,bh and bo: 
			Are network parameters.
	
	"""

    dW1 = np.zeros_like(W1)
    dW2 = np.zeros_like(W2)
    dW3 = np.zeros_like(W3)
    # must have the shape(batch, hiddensize)
    dbh = np.zeros_like(bh)
    # must have the shape(batch, outputsize)
    dbo = np.zeros_like(bo)
    dh = np.zeros_like(H[:, 0, :])

    _, T_x , _= Xt.shape
    loss = 0

    for t in reversed(range(T_x)):
        dw1, dw2, dw3, dbh, dbo, dh_prev, per_ts_loss = rnn_cell_backward(Xt[:, t, :],
																		 H[:, t, :],
																		 H[:, t - 1, :],
																		 O[:, t, :],
																		 labels[:, t, :],
																		 dh,
																		 W1, W2,W3 )
        dh = dh_prev

        dW1 += dw1
        dW2 += dw2
        dW3 += dw3
        dbh += dbh
        dbo += dbo
        
        # Update the loss by substracting the cross-entropy term of this time-step from it.
        loss -= np.log(per_ts_loss)

    return dW1, dW2, dW3, dbh, dbo, dh, loss

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

def rnn_cell_backward(xt,

h_prev,

output,

true_label,

h_gradient_or_dh,

W1,

W2,

W3 ):

"""

xt:

is the input in the form of (batch_size, input_dim_size)

h :

is the next hidden state

h_prev:

is the previous hidden state

output:

is the output of the rnn cell!

true_label:

is the true label for the current output

h_gradient_or_dh:

The dh which in the beginning is zero

and is updated as we go backward in the backprogagation.

the dh for the next round, would come from the dh_prev.

remember the backward pass is essentially a loop! and we

start at the end and traverse back to the beginning!

"""

e = np.copy(output)

# This is error_t = output_t - label_t

e[np.arange(e.shape[0]), np.argmax(true_label, axis=1)] -=1

# This is used for our loss to see how well we are doing during training.

per_ts_loss = output[np.arange(output.shape[0]), np.argmax(true_label, axis=1)].sum()

# this is the non-vectorized version of the above snippet

# per_ts_loss = 0

# for i, idx in enumerate(np.argmax(true_label, axis=1)):

# e[i, idx] -=1

# per_ts_loss += output[i, idx]

dW3 = np.dot(e.T, h)

# when calculating the dh, we also add the dh from the next timestep as well

# when we are in the last timestep, the h_gradient_or_dh is initially zero.

dh = np.dot(e, W3) + h_gradient_or_dh

# dbo = e.1, since we have batch we use np.sum

# e is a vector, when it is subtracted from label, the result will be added to dbo

dbo = np.sum(e, axis=0)

# the input part

dtanh = (1 - h * h) * dh

# compute the gradient of the loss with respect to W1

# this is actually not needed! bcause Xt is not a tunable

# parameter, thererfore we dont need it gradient.

# dxt = np.dot(dtanh, W1.T)

# must have the shape of (input_dim_size, hidden_state_size)

dW1 = np.dot(xt.T, dtanh)

# compute the gradient with respect to W2

dh_prev = np.dot(dtanh, W2.T)

# shape must be (HiddenSize, HiddenSize)

dW2 = np.dot(h_prev.T, dtanh)

# dbh += dtanh.1, we use sum, since we have a batch

dbh = np.sum(dtanh, axis=0)

return dW1, dW2, dW3, dbh, dbo, dh_prev, per_ts_loss

def rnn_layer_backward( Xt,

labels,

W1,

W2,

W3,

bh,

bo ):

"""

Xt:

The input in the form of (batch_size, time-step, input_dim_size)

labels:

The labels for each output with the shape (batch_size, time-step, outputsize)

H :

All the hidden states from the forward pass with the shape (batch_size, time-step, hidden_state_size)

All the outputs from the forward pass

W1,W2,W3,bh and bo:

Are network parameters.

"""

dW1 = np.zeros_like(W1)

dW2 = np.zeros_like(W2)

dW3 = np.zeros_like(W3)

# must have the shape(batch, hiddensize)

dbh = np.zeros_like(bh)

# must have the shape(batch, outputsize)

dbo = np.zeros_like(bo)

dh = np.zeros_like(H[:, 0, :])

_, T_x , _= Xt.shape

loss = 0

for t in reversed(range(T_x)):

dw1, dw2, dw3, dbh, dbo, dh_prev, per_ts_loss = rnn_cell_backward(Xt[:, t, :],

H[:, t, :],

H[:, t - 1, :],

O[:, t, :],

labels[:, t, :],

dh,

W1, W2,W3 )

dh = dh_prev

dW1 += dw1

dW2 += dw2

dW3 += dw3

dbh += dbh

dbo += dbo

# Update the loss by substracting the cross-entropy term of this time-step from it.

loss -= np.log(per_ts_loss)

return dW1, dW2, dW3, dbh, dbo, dh, loss

به منظور تست توابع پیاده سازی شده نیز میتوان بصورت زیر عمل کرد :


import numpy as np
np.random.seed(1)
input_dim_size = 3
hidden_state_size = 5
outputsize = 3
batch = 2
timesteps = 4

W1 = np.random.randn(input_dim_size, hidden_state_size)
W2 = np.random.randn(hidden_state_size, hidden_state_size)
W3 = np.random.randn(outputsize, hidden_state_size)
bh = np.random.randn(hidden_state_size)
bo = np.random.randn(outputsize)

Xt = np.random.rand(batch, timesteps, input_dim_size)
# label has the same shape as input, because we are creating outputs just like the inputs. 
Labels = np.random.rand(batch, timesteps, input_dim_size)
h_previous = np.zeros(shape=(batch, hidden_state_size))

Outputs, HiddenStates = rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3,bh, bo)
dW1, dW2, dW3, dbh, dbo, dh, loss = rnn_layer_backward(Xt, Labels, HiddenStates, Outputs,W1, W2, W3,bh, bo )
print(dW1.shape)
print("dh_prev[0] =", dh[0])
print("dh.shape =", dh.shape)
print("dW1[0] =", dW1[0])
print("dW1.shape =", dW1.shape)
print("dW2[0] =", dW2[0])
print("dW2.shape =", dW2.shape)
print("dbh[0] =", dbh[0])
print("dbh.shape =", dbh.shape)

import numpy as np

np.random.seed(1)

input_dim_size = 3

hidden_state_size = 5

outputsize = 3

batch = 2

timesteps = 4

W1 = np.random.randn(input_dim_size, hidden_state_size)

W2 = np.random.randn(hidden_state_size, hidden_state_size)

W3 = np.random.randn(outputsize, hidden_state_size)

bh = np.random.randn(hidden_state_size)

bo = np.random.randn(outputsize)

Xt = np.random.rand(batch, timesteps, input_dim_size)

# label has the same shape as input, because we are creating outputs just like the inputs.

Labels = np.random.rand(batch, timesteps, input_dim_size)

h_previous = np.zeros(shape=(batch, hidden_state_size))

Outputs, HiddenStates = rnn_layer_forward(Xt, hidden_state_size, W1, W2, W3,bh, bo)

dW1, dW2, dW3, dbh, dbo, dh, loss = rnn_layer_backward(Xt, Labels, HiddenStates, Outputs,W1, W2, W3,bh, bo )

print(dW1.shape)

print("dh_prev[0] =", dh[0])

print("dh.shape =", dh.shape)

print("dW1[0] =", dW1[0])

print("dW1.shape =", dW1.shape)

print("dW2[0] =", dW2[0])

print("dW2.shape =", dW2.shape)

print("dbh[0] =", dbh[0])

print("dbh.shape =", dbh.shape)

خروجی :


(3, 5)
dh_prev[0] = [-0.44595092 -0.0868595  -0.77449515 -0.50100593  0.35927758]
dh.shape = (2, 5)
dW1[0] = [-1.96168867  0.86751548  5.07050684  0.13683888  0.24913199]
dW1.shape = (3, 5)
dW2[0] = [-0.70572562 -0.53948113 -0.28133053  1.30360588  0.15237789]
dW2.shape = (5, 5)
dbh[0] = -3.859417642155729
dbh.shape = (5,)

(3, 5)

dh_prev[0] = [-0.44595092 -0.0868595 -0.77449515 -0.50100593 0.35927758]

dh.shape = (2, 5)

dW1[0] = [-1.96168867 0.86751548 5.07050684 0.13683888 0.24913199]

dW1.shape = (3, 5)

dW2[0] = [-0.70572562 -0.53948113 -0.28133053 1.30360588 0.15237789]

dW2.shape = (5, 5)

dbh[0] = -3.859417642155729

dbh.shape = (5,)

پیاده سازی کامل :

در نهایت تمام پیاده سازی ما بصورت زیر خواهد بود :


# in the name of Allah
import numpy as np

from sklearn.utils.extmath import softmax

class RNNClass(object):
    def __init__(self, input_dim_size, outputsize, hidden_state_size=100, mode=1, clipping_threshold=0.5):

        np.random.seed(1)

        # weights and biases - primitive method!
        self.W1 = np.random.randn(input_dim_size, hidden_state_size) * 0.01
        self.W2 = np.random.randn(hidden_state_size, hidden_state_size) * 0.01
        self.W3 = np.random.randn(outputsize, hidden_state_size) * 0.01

        # to fight vanishing gradient to some extend, we need proper weight initialization
        # Xavier-Glorot initialization
        # self.W1 = np.random.uniform( -np.sqrt(1./input_dim_size), np.sqrt(1./input_dim_size),(input_dim_size, hidden_state_size))
        # self.W2 = np.random.uniform( -np.sqrt(1./hidden_state_size), np.sqrt(1./hidden_state_size),(hidden_state_size, hidden_state_size) )
        # self.W3 = np.random.uniform( -np.sqrt(1./hidden_state_size), np.sqrt(1./hidden_state_size),(outputsize, hidden_state_size) )

        # This can be zero, it can also be randomly initialized
        self.bh = np.ones(shape=(hidden_state_size))
        self.bo = np.ones(shape=(outputsize))

        self.input_dim_size = input_dim_size
        self.outputsize = outputsize
        self.hidden_state_size = hidden_state_size

        self.mode = mode
        self.clipping_threshold = clipping_threshold

        print('W1: ', self.W1.shape)
        print('W2: ', self.W2.shape)
        print('W3: ', self.W3.shape)
        print('bh: ', self.bh.shape)
        print('bo: ', self.bo.shape)

    def rnn_cell_foward(self, xt, h0):
        """
            Run the forward pass for a single timestep of a vanilla RNN that uses a tanh
            activation function.
            The input data has dimension D(vocabsize in case we have nlp use), the hidden state
            has dimension H, and we use a minibatch size of N.
            Inputs:
            - x: Input data for this timestep, of shape (Batch_size, vocabsize_or_basically_input_dim_size).
            - h0: Hidden state from previous timestep, of shape (Batch_size, HiddenSize)

            Returns :
            - h_t: Next hidden state, of shape (Batch_size, HiddenSize)
            - output: output , of shape (Batch_size, outputsize)
       """

        h_t = np.tanh(np.dot(xt, self.W1) + np.dot(h0, self.W2) + self.bh)
        o = np.dot(h_t, self.W3.T) + self.bo
        o_t = softmax(o)

        return o_t, h_t

    def rnn_layer_forward(self, Xt, H=None):
        """
            Runs a forward pass on the input data Xt and optional hiddenstate H.
            if H is initialized, the initial hiddenstate (h0) will be initialized
            from the last hiddenstate using this optional argument.
            Inputs:
            - Xt: The input data of shape (Batch_size, time_steps, input_dim_size)
            - H(Optional): an array containing hiddenstates from previous example
              of shape(Batch_size, timesteps, HiddenStateSize)

            Returns :
            - O: The output for the current layer of shape (Batch_size, timesteps, outputsize)
            - H: The hiddenstates for the current layer of shape (Batch_size, timesteps, HiddenStateSize)

        """

        batch, T_x, input_dim_size = Xt.shape
        H = np.zeros(shape=(batch, T_x, self.hidden_state_size))
        O = np.zeros(shape=(batch, T_x, self.outputsize))

        if (self.mode == 1):
            h_previous = np.zeros(shape=(batch, self.hidden_state_size))
        else:
            h_previous = H[:, -1, :]

        for t in range(T_x):
            output, h_t = self.rnn_cell_foward(Xt[:, t, :], h_previous)
            H[:, t, :] = h_t
            O[:, t, :] = output

            # Our current/new hiddenstate will be the previous hiddenstate for the next round,
            h_previous = h_t

        return O, H

    def rnn_cell_backward(self, xt, h, h_prev, output, true_label, dh_next):
        """
            Runs a single backward pass once.
            Inputs:
            - xt: The input data of shape (Batch_size, input_dim_size)
            - h:  The next hidden state at timestep t(which come from the forward pass)
            - h_prev: The previous hidden state at timestep t-1
            - output : The output at the current timestep
            - true_label: The label for the current timestep, used for calcuating loss
            - dh_next: The gradient of hiddent state h (dh) which in the beginning
                is zero and is updated as we go backward in the backprogagation.
                the dh for the next round, would come from the 'dh_prev' as we will see shortly!
                Just remember the backward pass is essentially a loop! and we start at the end 
                and traverse back to the beginning!

            Returns : 
            - dW1 : The gradient for W1
            - dW2 : The gradient for W2
            - dW3 : The gradient for W3
            - dbh : The gradient for bh
            - dbo : The gradient for bo
            - dh_prev : The gradient for previous hiddenstate at timestep t-1. this will be used
            as the next dh for the next round of backpropagation.
            - per_ts_loss  : The loss for current timestep.
        """
        e = np.copy(output)
        # correct idx for each row(sample)!
        idxs = np.argmax(true_label, axis=1)
        # number of rows(samples) in our batch
        rows = np.arange(e.shape[0])
        # This is the vectorized version of error_t = output_t - label_t or simply e = output[t] - 1
        # where t refers to the index in which label is 1. 
        e[rows, idxs] -= 1
        # This is used for our loss to see how well we are doing during training.
        per_ts_loss = output[rows, idxs].sum()

        # must have shape of W3 which is (vocabsize_or_output_dim_size, hidden_state_size)
        dW3 = np.dot(e.T, h)
        # dbo = e.1, since we have batch we use np.sum
        # e is a vector, when it is subtracted from label, the result will be added to dbo
        dbo = np.sum(e, axis=0)
        # when calculating the dh, we also add the dh from the next timestep as well
        # when we are in the last timestep, the dh_next is initially zero.
        dh = np.dot(e,  self.W3) + dh_next  # from later cell
        # the input part
        dtanh = (1 - h * h) * dh
        # dbh = dtanh.1, we use sum, since we have a batch
        dbh = np.sum(dtanh, axis=0)

        # compute the gradient of the loss with respect to W1
        # this is actually not needed! we only care about tunable
        # parameters, so we are only after, W1,W2,W3, db and do
        # dxt = np.dot(dtanh, W1.T)

        # must have the shape of (vocab_size, hidden_state_size)
        dW1 = np.dot(xt.T, dtanh)
        # shape must be (HiddenSize, HiddenSize)
        dW2 = np.dot(h_prev.T, dtanh)
        # compute the gradient with respect to W2
        dh_prev = np.dot(dtanh, self.W2.T)


        return dW1, dW2, dW3, dbh, dbo, dh_prev, per_ts_loss

    def rnn_layer_backward(self, Xt, labels, H, O):
        """
            Runs a full backward pass on the given data. and returns the gradients.
            Inputs: 
            - Xt: The input data of shape (Batch_size, timesteps, input_dim_size)
            - labels: The labels for the input data
            - H: The hiddenstates for the current layer prodced in the foward pass 
              of shape (Batch_size, timesteps, HiddenStateSize)
            - O: The output for the current layer of shape (Batch_size, timesteps, outputsize)

            Returns :
            - dW1: The gradient for W1
            - dW2: The gradient for W2
            - dW3: The gradient for W3
            - dbh: The gradient for bh
            - dbo: The gradient for bo
            - dh: The gradient for the hidden state at timestep t
            - loss: The current loss 

        """

        dW1 = np.zeros_like(self.W1)
        dW2 = np.zeros_like(self.W2)
        dW3 = np.zeros_like(self.W3)
        dbh = np.zeros_like(self.bh)
        dbo = np.zeros_like(self.bo)
        dh_next = np.zeros_like(H[:, 0, :])
        hprev = None

        batchsz, T_x, inptdm = Xt.shape
        loss = 0
        for t in reversed(range(T_x)):

            # this if-else block can be removed! and for hprev, we can simply
            # use H[:,t -1, : ] instead, but I also add this in case it makes a
            # a difference! so far I have not seen any difference though!
            if t > 0:
                hprev = H[:, t - 1, :]
            else:
                hprev = np.zeros_like(H[:, 0, :])

            dw_1, dw_2, dw_3, db_h, db_o, dh_prev, e = self.rnn_cell_backward(Xt[:, t, :],
                                                                              H[:, t, :],
                                                                              hprev,
                                                                              O[:, t, :],
                                                                              labels[:, t, :],
                                                                              dh_next)
            dh_next = dh_prev
            dW1 += dw_1
            dW2 += dw_2
            dW3 += dw_3
            dbh += db_h[0]
            dbo += db_o

            # Update the loss by substracting the cross-entropy term of this time-step from it.
            loss -= np.log(e)

        return dW1, dW2, dW3, dbh, dbo, dh_next, loss

    def update_parameters(self, dW1, dW2, dW3, dbh, dbo, lr):
        """
            Updates the parameters. 
            Inputs:
            - lr : the learning rate used for updaing the parameters. 
            - dW1: The gradient for W1
            - dW2: The gradient for W2
            - dW3: The gradient for W3
            - dbh: The gradient for bh
            - dbo: The gradient for bo

            Returns : 
            - W1: The updated W1
            - W2: The updated W2
            - W3: The updated W3
            - bh: The updated bh
            - bo: The updated bo
        """

        self.W1 += -lr * dW1
        self.W2 += -lr * dW2
        self.W3 += -lr * dW3
        self.bh += -lr * dbh
        self.bo += -lr * dbo

        return self.W1, self.W2, self.W3, self.bh, self.bo

    def clip(self, dW1, dW2, dW3, dbh, dbo, maxValue=0.5):
        '''
        Clips the gradients' values between minimum and maximum.
        Arguments:
        The gradients "dW1", "dW2", "dW3", "db", "dby"
        maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
        Returns: 
        gradients -- "dW1", "dW2", "dW3", "db", "dby"
        '''
        for gradient in [dW1, dW2, dW3, dbh, dbo]:
            np.clip(gradient, a_min=-maxValue, a_max=maxValue, out=gradient)

        return dW1, dW2, dW3, dbh, dbo

    def optimize(self, X, Y, H, learning_rate=0.01):
        """
            Runs a complete forward-backward pass and then updates
            The weights.
            Inputs:
            - X: The input data of shape (Batch_size, time_steps, input_dim_size)
            - Y: The labels for the input data of shape (Batch_size, time_steps, outputsize)
            - H: (Optional), The hiddenstates of shape (Batchsize, timesteps, hiddenstateSize)
              that you can provide, so that in the forward pass, the initial hiddenstate uses
              its last timestep hiddenstate for the previous examples forward pass. Initially 
              array must be all zeros, then after the first fowardpass, you return the resulting 
              H, and for the next round, use that H! We will see how this works when we try to 
              use our class on a test data!

            Returns : 
            - loss
            - dW1: The gradient for W1
            - dW2: The gradient for W2
            - dW3: The gradient for W3
            - dbh: The gradient for bh
            - dbo: The gradient for bo
            - H: The hiddenstates for this round of forward pas

        """

        # Forward propagate through time
        O, H = self.rnn_layer_forward(X, H)

        # Backpropagate through time
        dW1, dW2, dW3, dbh, dbo, dh, loss = self.rnn_layer_backward(X, Y, H, O)


        #dW1, dW2, dW3, dbh, dbo = self.clip( dW1, dW2, dW3, dbh, dbo, maxValue=self.clipping_threshold)


        # Update parameters
        W1, dW2, dW3, dbh, dbo = self.update_parameters( dW1, dW2, dW3, dbh, dbo, learning_rate)

        return loss, dW1, dW2, dW3, dbh, dbo, H

    def gradient_checking(self, X, Y, epsilon=1e-5):

        # Forward propagate through time
        O, H = self.rnn_layer_forward(X, H=None)
        # Backpropagate through time
        dW1, dW2, dW3, dbh, dbo, dh, loss = self.rnn_layer_backward(X, Y, H, O)

        for param, dparam, name in zip([self.W1, self.W2, self.W3, self.bh, self.bo],
                                       [dW1,     dW2,     dW3,     dbh,      dbo],
                                       ['W1',    'W2',    'W3',    'bh',     'bo']):
            s0 = param.shape
            s1 = dparam.shape

            assert s0 == s1, 'Error! @ {} dimensions must match! and here {} != {} '.format(name, s0, s1)

            print('{}:'.format(name))

            # number of checks for each parameter
            num_checks = 3

            for i in range(num_checks):

                ri = int(np.random.uniform(0, param.size))
                old_val = param.flat[ri]

                param.flat[ri] = old_val + epsilon

                # Forward propagate through time
                O, H = self.rnn_layer_forward(X, H=None)
                # Backpropagate through time
                dW1, dW2, dW3, dbh, dbo, dh, loss0 = self.rnn_layer_backward( X, Y, H, O)

                param.flat[ri] = old_val - epsilon

                # Forward propagate through time
                O, H = self.rnn_layer_forward(X, H=None)
                # Backpropagate through time
                dW1, dW2, dW3, dbh, dbo, dh, loss1 = self.rnn_layer_backward( X, Y, H, O)

                # restore the original value
                param.flat[ri] = old_val

                grad_analytical = dparam.flat[ri]
                grad_numerical = (loss0 - loss1) / (2 * epsilon)

                relative_error = abs(
                    grad_analytical - grad_numerical) / abs(grad_numerical + grad_analytical)

                print('{}, {} => error: {} (error should be less than {})'.format(
                    grad_analytical, grad_numerical, relative_error, 1e-7))

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

321

322

323

324

325

326

327

328

329

330

331

332

333

334

335

336

337

338

339

340

341

342

343

344

345

346

347

348

349

350

# in the name of Allah

import numpy as np

from sklearn.utils.extmath import softmax

class RNNClass(object):

def __init__(self, input_dim_size, outputsize, hidden_state_size=100, mode=1, clipping_threshold=0.5):

np.random.seed(1)

# weights and biases - primitive method!

self.W1 = np.random.randn(input_dim_size, hidden_state_size) * 0.01

self.W2 = np.random.randn(hidden_state_size, hidden_state_size) * 0.01

self.W3 = np.random.randn(outputsize, hidden_state_size) * 0.01

# to fight vanishing gradient to some extend, we need proper weight initialization

# Xavier-Glorot initialization

# self.W1 = np.random.uniform( -np.sqrt(1./input_dim_size), np.sqrt(1./input_dim_size),(input_dim_size, hidden_state_size))

# self.W2 = np.random.uniform( -np.sqrt(1./hidden_state_size), np.sqrt(1./hidden_state_size),(hidden_state_size, hidden_state_size) )

# self.W3 = np.random.uniform( -np.sqrt(1./hidden_state_size), np.sqrt(1./hidden_state_size),(outputsize, hidden_state_size) )

# This can be zero, it can also be randomly initialized

self.bh = np.ones(shape=(hidden_state_size))

self.bo = np.ones(shape=(outputsize))

self.input_dim_size = input_dim_size

self.outputsize = outputsize

self.hidden_state_size = hidden_state_size

self.mode = mode

self.clipping_threshold = clipping_threshold

print('W1: ', self.W1.shape)

print('W2: ', self.W2.shape)

print('W3: ', self.W3.shape)

print('bh: ', self.bh.shape)

print('bo: ', self.bo.shape)

def rnn_cell_foward(self, xt, h0):

"""

Run the forward pass for a single timestep of a vanilla RNN that uses a tanh

activation function.

The input data has dimension D(vocabsize in case we have nlp use), the hidden state

has dimension H, and we use a minibatch size of N.

Inputs:

- x: Input data for this timestep, of shape (Batch_size, vocabsize_or_basically_input_dim_size).

- h0: Hidden state from previous timestep, of shape (Batch_size, HiddenSize)

Returns :

- h_t: Next hidden state, of shape (Batch_size, HiddenSize)

- output: output , of shape (Batch_size, outputsize)

"""

h_t = np.tanh(np.dot(xt, self.W1) + np.dot(h0, self.W2) + self.bh)

o = np.dot(h_t, self.W3.T) + self.bo

o_t = softmax(o)

return o_t, h_t

def rnn_layer_forward(self, Xt, H=None):

"""

Runs a forward pass on the input data Xt and optional hiddenstate H.

if H is initialized, the initial hiddenstate (h0) will be initialized

from the last hiddenstate using this optional argument.

Inputs:

- Xt: The input data of shape (Batch_size, time_steps, input_dim_size)

- H(Optional): an array containing hiddenstates from previous example

of shape(Batch_size, timesteps, HiddenStateSize)

Returns :

- O: The output for the current layer of shape (Batch_size, timesteps, outputsize)

- H: The hiddenstates for the current layer of shape (Batch_size, timesteps, HiddenStateSize)

"""

batch, T_x, input_dim_size = Xt.shape

H = np.zeros(shape=(batch, T_x, self.hidden_state_size))

O = np.zeros(shape=(batch, T_x, self.outputsize))

if (self.mode == 1):

h_previous = np.zeros(shape=(batch, self.hidden_state_size))

else:

h_previous = H[:, -1, :]

for t in range(T_x):

output, h_t = self.rnn_cell_foward(Xt[:, t, :], h_previous)

H[:, t, :] = h_t

O[:, t, :] = output

# Our current/new hiddenstate will be the previous hiddenstate for the next round,

h_previous = h_t

return O, H

def rnn_cell_backward(self, xt, h, h_prev, output, true_label, dh_next):

"""

Runs a single backward pass once.

Inputs:

- xt: The input data of shape (Batch_size, input_dim_size)

- h: The next hidden state at timestep t(which come from the forward pass)

- h_prev: The previous hidden state at timestep t-1

- output : The output at the current timestep

- true_label: The label for the current timestep, used for calcuating loss

- dh_next: The gradient of hiddent state h (dh) which in the beginning

is zero and is updated as we go backward in the backprogagation.

the dh for the next round, would come from the 'dh_prev' as we will see shortly!

Just remember the backward pass is essentially a loop! and we start at the end

and traverse back to the beginning!

Returns :

- dW1 : The gradient for W1

- dW2 : The gradient for W2

- dW3 : The gradient for W3

- dbh : The gradient for bh

- dbo : The gradient for bo

- dh_prev : The gradient for previous hiddenstate at timestep t-1. this will be used

as the next dh for the next round of backpropagation.

- per_ts_loss : The loss for current timestep.

"""

e = np.copy(output)

# correct idx for each row(sample)!

idxs = np.argmax(true_label, axis=1)

# number of rows(samples) in our batch

rows = np.arange(e.shape[0])

# This is the vectorized version of error_t = output_t - label_t or simply e = output[t] - 1

# where t refers to the index in which label is 1.

e[rows, idxs] -= 1

# This is used for our loss to see how well we are doing during training.

per_ts_loss = output[rows, idxs].sum()

# must have shape of W3 which is (vocabsize_or_output_dim_size, hidden_state_size)

dW3 = np.dot(e.T, h)

# dbo = e.1, since we have batch we use np.sum

# e is a vector, when it is subtracted from label, the result will be added to dbo

dbo = np.sum(e, axis=0)

# when calculating the dh, we also add the dh from the next timestep as well

# when we are in the last timestep, the dh_next is initially zero.

dh = np.dot(e, self.W3) + dh_next # from later cell

# the input part

dtanh = (1 - h * h) * dh

# dbh = dtanh.1, we use sum, since we have a batch

dbh = np.sum(dtanh, axis=0)

# compute the gradient of the loss with respect to W1

# this is actually not needed! we only care about tunable

# parameters, so we are only after, W1,W2,W3, db and do

# dxt = np.dot(dtanh, W1.T)

# must have the shape of (vocab_size, hidden_state_size)

dW1 = np.dot(xt.T, dtanh)

# shape must be (HiddenSize, HiddenSize)

dW2 = np.dot(h_prev.T, dtanh)

# compute the gradient with respect to W2

dh_prev = np.dot(dtanh, self.W2.T)

return dW1, dW2, dW3, dbh, dbo, dh_prev, per_ts_loss

def rnn_layer_backward(self, Xt, labels, H, O):

"""

Runs a full backward pass on the given data. and returns the gradients.

Inputs:

- Xt: The input data of shape (Batch_size, timesteps, input_dim_size)

- labels: The labels for the input data

- H: The hiddenstates for the current layer prodced in the foward pass

of shape (Batch_size, timesteps, HiddenStateSize)

- O: The output for the current layer of shape (Batch_size, timesteps, outputsize)

Returns :

- dW1: The gradient for W1

- dW2: The gradient for W2

- dW3: The gradient for W3

- dbh: The gradient for bh

- dbo: The gradient for bo

- dh: The gradient for the hidden state at timestep t

- loss: The current loss

"""

dW1 = np.zeros_like(self.W1)

dW2 = np.zeros_like(self.W2)

dW3 = np.zeros_like(self.W3)

dbh = np.zeros_like(self.bh)

dbo = np.zeros_like(self.bo)

dh_next = np.zeros_like(H[:, 0, :])

hprev = None

batchsz, T_x, inptdm = Xt.shape

loss = 0

for t in reversed(range(T_x)):

# this if-else block can be removed! and for hprev, we can simply

# use H[:,t -1, : ] instead, but I also add this in case it makes a

# a difference! so far I have not seen any difference though!

if t > 0:

hprev = H[:, t - 1, :]

else:

hprev = np.zeros_like(H[:, 0, :])

dw_1, dw_2, dw_3, db_h, db_o, dh_prev, e = self.rnn_cell_backward(Xt[:, t, :],

H[:, t, :],

hprev,

O[:, t, :],

labels[:, t, :],

dh_next)

dh_next = dh_prev

dW1 += dw_1

dW2 += dw_2

dW3 += dw_3

dbh += db_h[0]

dbo += db_o

# Update the loss by substracting the cross-entropy term of this time-step from it.

loss -= np.log(e)

return dW1, dW2, dW3, dbh, dbo, dh_next, loss

def update_parameters(self, dW1, dW2, dW3, dbh, dbo, lr):

"""

Updates the parameters.

Inputs:

- lr : the learning rate used for updaing the parameters.

- dW1: The gradient for W1

- dW2: The gradient for W2

- dW3: The gradient for W3

- dbh: The gradient for bh

- dbo: The gradient for bo

Returns :

- W1: The updated W1

- W2: The updated W2

- W3: The updated W3

- bh: The updated bh

- bo: The updated bo

"""

self.W1 += -lr * dW1

self.W2 += -lr * dW2

self.W3 += -lr * dW3

self.bh += -lr * dbh

self.bo += -lr * dbo

return self.W1, self.W2, self.W3, self.bh, self.bo

def clip(self, dW1, dW2, dW3, dbh, dbo, maxValue=0.5):

'''

Clips the gradients' values between minimum and maximum.

Arguments:

The gradients "dW1", "dW2", "dW3", "db", "dby"

maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue

Returns:

gradients -- "dW1", "dW2", "dW3", "db", "dby"

'''

for gradient in [dW1, dW2, dW3, dbh, dbo]:

np.clip(gradient, a_min=-maxValue, a_max=maxValue, out=gradient)

return dW1, dW2, dW3, dbh, dbo

def optimize(self, X, Y, H, learning_rate=0.01):

"""

Runs a complete forward-backward pass and then updates

The weights.

Inputs:

- X: The input data of shape (Batch_size, time_steps, input_dim_size)

- Y: The labels for the input data of shape (Batch_size, time_steps, outputsize)

- H: (Optional), The hiddenstates of shape (Batchsize, timesteps, hiddenstateSize)

that you can provide, so that in the forward pass, the initial hiddenstate uses

its last timestep hiddenstate for the previous examples forward pass. Initially

array must be all zeros, then after the first fowardpass, you return the resulting

H, and for the next round, use that H! We will see how this works when we try to

use our class on a test data!

Returns :

- loss

- dW1: The gradient for W1

- dW2: The gradient for W2

- dW3: The gradient for W3

- dbh: The gradient for bh

- dbo: The gradient for bo

- H: The hiddenstates for this round of forward pas

"""

# Forward propagate through time

O, H = self.rnn_layer_forward(X, H)

# Backpropagate through time

dW1, dW2, dW3, dbh, dbo, dh, loss = self.rnn_layer_backward(X, Y, H, O)

#dW1, dW2, dW3, dbh, dbo = self.clip( dW1, dW2, dW3, dbh, dbo, maxValue=self.clipping_threshold)

# Update parameters

W1, dW2, dW3, dbh, dbo = self.update_parameters( dW1, dW2, dW3, dbh, dbo, learning_rate)

return loss, dW1, dW2, dW3, dbh, dbo, H

def gradient_checking(self, X, Y, epsilon=1e-5):

# Forward propagate through time

O, H = self.rnn_layer_forward(X, H=None)

# Backpropagate through time

dW1, dW2, dW3, dbh, dbo, dh, loss = self.rnn_layer_backward(X, Y, H, O)

for param, dparam, name in zip([self.W1, self.W2, self.W3, self.bh, self.bo],

[dW1, dW2, dW3, dbh, dbo],

['W1', 'W2', 'W3', 'bh', 'bo']):

s0 = param.shape

s1 = dparam.shape

assert s0 == s1, 'Error! @ {} dimensions must match! and here {} != {} '.format(name, s0, s1)

print('{}:'.format(name))

# number of checks for each parameter

num_checks = 3

for i in range(num_checks):

ri = int(np.random.uniform(0, param.size))

old_val = param.flat[ri]

param.flat[ri] = old_val + epsilon

# Forward propagate through time

O, H = self.rnn_layer_forward(X, H=None)

# Backpropagate through time

dW1, dW2, dW3, dbh, dbo, dh, loss0 = self.rnn_layer_backward( X, Y, H, O)

param.flat[ri] = old_val - epsilon

# Forward propagate through time

O, H = self.rnn_layer_forward(X, H=None)

# Backpropagate through time

dW1, dW2, dW3, dbh, dbo, dh, loss1 = self.rnn_layer_backward( X, Y, H, O)

# restore the original value

param.flat[ri] = old_val

grad_analytical = dparam.flat[ri]

grad_numerical = (loss0 - loss1) / (2 * epsilon)

relative_error = abs(

grad_analytical - grad_numerical) / abs(grad_numerical + grad_analytical)

print('{}, {} => error: {} (error should be less than {})'.format(

grad_analytical, grad_numerical, relative_error, 1e-7))

در پیاده سازی فوق ما مفاهیم پایه را در نظر گرفتیم . مفاهیمی همانند truncated backpropagation و مباحث مرتبط با مقداردهی اولیه و بحث محوشدگی گرادیان(روشهای مقابله با آن همانند Gradient clipping و…) بعد از بیان مفاهیم پایه بعدی در پستی جداگانه بیان میشوند.

نکته پیاده سازی(پس انتشار در زمان و پس انتشار کوتاه شده در زمان)

در زیر مروری بر این مفاهیم داریم و انشاءالله در مطلبی جداگانه بصورت کامل به این مباحث خواهیم پرداخت.

پس انتشار در زمان (Backpropagation Through Time ) :

عملیات پس انتشار در یک شبکه عصبی بازگشتی تا حد بسیار زیادی همانند آنچه در شبکه های عصبی سنتی رخ میدهد است. اما در این نوع شبکه ها ما نیازمند آن هستیم که خطاها را از سلول فعلی به سلول های قبلی نیز منتقل کنیم. این همان قابلیتی است به شبکه عصبی بازگشتی اجازه حفظ و ثبت وابستگی های زمانی بلند مدت را میدهد. از آنجایی که ما درگیر گام های زمانی مختلف هستیم به این انتقال خطا از سلول فعلی به سلولهای قبلی (در طول زمان) پس انتشار در زمان (بک پراپگیشن در زمان) گفته میشود. از انجایی که پارامترهای مدل ما در این نوع شبکه ها در بین سلولهای مختلف بصورت مشترک اند (هر سلول RNN دقیقا از یک مجموعه وزن و بایاس بهره میبرد)، ما باید گرادایان ها را با توجه به هر گام زمانی بصورت جداگانه محاسبه کرده و سپس آن ها را با یکدیگر جمع کنیم. مشابه این روش را در شبکه های عصبی دیگری که دارای اشتراک پارامتر هستند (همانند شبکه های عصبی کانولوشن) نیز مشاهده میکنیم.

پس انتشار در زمان یا اصطلاحا Backpropagation through time (یا بصورت اختصار BPTT ) شیوه ای است که برای آموزش شبکه های عصبی بازگشتی مورد استفاده قرار میگیرد. این روش اما در زمان استفاده از دنباله های بسیار طولانی با مشکلاتی مواجه است. یادگیری یک شبکه عصبی بازگشتی با الگوریتم پس انتشار در زمان نیازمند باز کردن(unfold) شبکه در زمان به تعداد تمامی گام های زمانی که در دنباله ورودی وجود دارد است. این مساله در دنباله های بسیار طولانی سبب تحمیل محاسبات بسیار سنگین و مصرف حافظه بسیاری میشود چرا که نیازمند پردازش تمامی دنباله ورودی هستیم تا نهایتا یک گرادیان بدست آید این کاستی در اغلب اوقات(زمانی که خروجی از نوع سری باشد) با کوتاه سازی دنباله ورودی به چند دنباله کوچکتر و اعمال پس انتشار در این زیردنباله ها برطرف میشود. این الگوریتم به پس انتشار کوتاه شده در زمان یا اصطلاحا turncated backpropagation through time یا به اختصار TBPTT معروف است. هرچند این روش مشکل سربار محاسباتی و حافظه را در الگوریتم اصلی برطرف میسازد اما باعث از دست دادن وابستگی های زمانی طولانی مدت نیز میشود.

الگوریتم پس انتشار در زمان و معادل کوتاه شده آن تقریبا در حوزه شبکه های عصبی بازگشتی بی رقیب هسند. “پس انتشار در زمان” تقریبا بر روی دنباله های بسیار طولانی بسختی قابل استفاده است چرا که نیازمند ذخیره سازی و پس انتشار در یک شبکه با تعداد بسیار زیاد گام زمانی است (که هرکدام را میتوانید در قالب یک لایه متصور شوید) که این مساله باعث مصرف حجم قابل توجهی از حافظه و تحمیل سربار پردازشی بسیار زیادی است. مصرف حافظه را میتوان بصورت جزئی همانطور که در مقاله Memory-efficient backpropagation throughtime آمده است با افزایش سربار پردازشی برطرف کرد. پس انتشار در دنباله های بسیار طولانی همچنین به معنای اعمال گام های گرادیان کاهشی(gradient descent) کمتری است که بطور قابل توجهی آموزش را کند میکند. الگوریتم پس انتشار کوتاه شده در زمان کاستی های الگوریتم “پس انتشار در زمان” را با تقسیم دنباله اولیه به چند زیر دنباله با اندازه مساوی برطرف میکند. “پس انتشار کوتاه شده در زمان” جریان گرادیان در بین زیر دنباله ها را کوتاه میکند اما حالت مخفی در شبکه را حفظ میکند. عمل کوتاه سازی باعث ایجاد گرایش(بایاس) در گرادیان ها شده و با اینکار هرگونه ضمانت همگرایی با زیربنای نظری را از بین میبرد. بطور شهودی پس انتشار کوتاه شده در زمان در یادگیری وابستگی هایی که بیش از اندازه کوتاه سازی است با مشکل مواجه است. روش هایی همانند NoBackTrack و Unbiased Online Recurrent Optimization(UORO) هر دو الگوریتم های یادگیری بازگشتی برخط بدون گرایش قابل تطبیقی را فراهم میکنند. این روشها نقطه نظر مقابل که نیازمند بدون حافظگی است را در پیش میگیرند بنابر این روشهای کوتاه سازی و هرگونه ذخیرهسازی حالات قبلی را غیرمجاز در نظر میگیرند. این روشها تماما برخط هستند و ساختار جریانی آنها باعث ایجاد تزریق نویز در تقریب گرادیان ها میشود.

منابع جهت مطالعه بیشتر :

https://www.cs.utoronto.ca/~ilya/pubs/ilya_sutskever_phd_thesis.pdf
https://arxiv.org/pdf/1705.08209.pdf
https://r2rt.com/styles-of-truncated-backpropagation.html
http://ir.hit.edu.cn/~jguo/docs/notes/bptt.pdf
https://r2rt.com/written-memories-understanding-deriving-and-extending-the-lstm.html#backpropagation-through-time-and-vanishing-sensitivity

در بخش بعد به معرفی GRU و بعد از آن LSTM خواهیم پرداخت.

9 نظرات

روش Teacher Forcing چیست؟ | یادگیری عمیق - Deep learning 6 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent neural network) بخش سوم : Backpr… […]
آموزش شبکه عصبی بازگشتی بخش پنجم : معرفی LSTM | یادگیری عمیق - Deep learning 6 سال پیش

[…] آموزش شبکه های عصبی بازگشتی (Recurrent neural network) بخش سوم : Backpr… […]
مهسا می گوید 5 سال پیش

e[np.arange(e.shape[0]), np.argmax(true_label, axis=1)] -=1
همانطور که توضیح داده اید خطا همان اختلاف خروجی شبکه در هر گام از مقدار واقعی همان گام است
اما من پیاده سازی که به صورت بالا گفته اید را متوجه نمیشوم
اگر امکان دارد این فرمول را بیشتر توضیح دهید
باتشکر

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  کدوم بخشش رو متوجه نمیشید؟
  بخش مرتبط با پایتون (این دستور چکار میکنه) یا اینکه کلا مفهوم این قطعه کد رو متوجه نمیشید؟
  
  پاسخ
مهسا می گوید 5 سال پیش

اگر true_lable=[[1,0,0],[0,0,1]] حال np.argmax(true_label, axis=1)=[0,2]
و اگر خروجی شبکه به صورت e=[[0,1,0],[1,0 ,0]] (در واقع هنوز اموزش ندیده است) حال e.shape[0]=2 و [
[۰,۱]=np.arange(e.shape[0])
حال من متوجه نمیشوم
e[[0,1],[0,2]]یعنی چه ؟ و پس از آن e[[0,1],[0,2]]-=1چطور اختلاف مقادیر خروجی و واقعی را محاسبه میکند؟

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  سلام
  کامنت های پیاده سازی نهایی که نوشتم رو بخونید متوجه میشید . این پیاده سازی vectorized هست . نمونه غیر برداری اون رو هم بصورت کامنت تو خط ۳۷ نوشتم که ببینید احتمالا کاملا متوجه میشید.
  بخش اول سطرها رو مشخص میکنه و بخش دوم اندیس جاهایی که لیبل ۱ هست . مثلا سطر ۰ اندیس ۰ ( و سطر ۱ اندیس ۲ )
  دقت بکنید میبینید سطر ۰ اندیس ۰ داره اطلاعات لیبل صحیح شما رو میده که برای نمونه اول (سطر اول) کدوم کلاس صحیح هست :
  true_lable=[[1,0,0],
  [۰,۰,۱]]
  
  لیبل مربوط به نمونه اول (سطر ۰) اندیس ۰ نشانگر کلاس صحیح هست .
  و در نمونه دوم (سطر ۱) هم اندیس ۲ نشانگر کلاس صحیح هست.
  حالا همین درایه ها از ۱ کسر میشن تا خطا محاسبه بشه. (در هر گام زمانی ما فقط دنبال این هستیم که ببینیم در اون گام کلاس صحیح انتخاب شده یا نه و این رو از طریق قیاس خروجی پیش بینی شده – لیبل (که در اصل همون ۱ هست) بدست میاریم.
  
  پاسخ
مهسا می گوید 5 سال پیش

یعنی اینجوری که شما میفرمایید اگر من درست متوجه شده باشم
داخل ماتریس eفقط طبق مثال درایه های (۰,۰)و (۱,۲) منهی یک میشوند اگر مقدار این درایه ها برابر یک شده باشند پس با کم کردن از یک میشه صفر و این یعنی ما کاملا شبکمون اموزش دیده و به همون لیبل ها رسیده درسته؟ ودیگه مقادیر پارامترها اپدیت نمیشوند (چون مشتقات صفر خواهند شد ) .
و خطا per_ts_loss به چه علت استفاده شده است؟

پاسخ
1. سید حسین حسن پور متی کلایی می گوید 5 سال پیش
  
  ما داریم خطای خروجی رو محاسبه میکنیم برای یک گام! اگر جمله شما ۵ کلمه باشه باید مشخص بشه ایا تمام کلمات درست تشخیص داده شدند یا نه. پس شما هر بار یک کلمه رو میبینید آیا درست بوده تشخیص یا نه. صرف این که یک گام زمانی خروجی صحیحی تولید کرده به معنای تنظیم بودن شبکه نیست. انقدر این مساله تکرار میشه تا خطای کلی نهایتا کمینه بشه.
  اون per_ts_loss هم برای محاسبه کراس انتروپی هست. کد رو ببینید مشخصه.
  
  پاسخ
مهسا می گوید 5 سال پیش

خیلی ممنون از توضیحاتتون

پاسخ

ارسال یک پاسخ

این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش می‌شوند.